2直線のなす角

2直線のなす角を\(\tan\)の加法定理を用いて求める方法にについて見ていきます。
まずは例題から始めて、最後に一般論について見ていきます。

(例題)
(1)2直線 \(3x-y+1=0\),  \(x-2y+4=0\) のなす角\(θ\) (\(0°≦θ≦90°\)) を求めよ。
(2)直線 \(y=-x+3\) と\(\displaystyle\frac{π}{3}\) の角をなす直線の傾きを求めよ。

(解答)
(1)

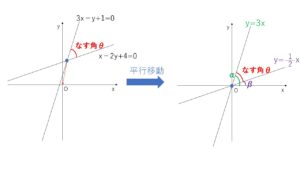
2直線の交点が原点にくるように平行移動すると、2直線は
\(y=3x\)・・・①,  \(y=\displaystyle\frac{1}{2}x\)・・・②

①,②と\(x\)軸の正の向きとなす角をそれぞれ\(α,β\) とすると
\(\tanα=3\),\(\tanβ=\displaystyle\frac{1}{2}\)

①②のなす角が求める角\(θ\)で、図よりそれは \(α-β\) となる。

ここで図より、\(α-β≠90°\) だから
\(\tan(α-β)\)\(=\displaystyle\frac{3-\displaystyle\frac{1}{2}}{1+3\cdot\displaystyle\frac{1}{2}}\)\(=1\)

\(0≦α-β≦90°\) より
\(θ\)\(=α-β\)\(=45°\)

(2)

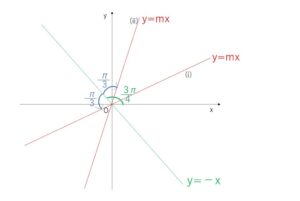
直線 \(x=k\) は条件を満たさないので、求める直線の傾きを\(m\)とすると、
\(y=-x\) と \(\displaystyle\frac{π}{3}\) の角をなす,直線 \(y=mx\) を考えればよい。

\(y=-x\) と\(x\)軸の正の向きとなす角は \(\displaystyle\frac{3}{4}π\) なので
\(m=\tan(\displaystyle\frac{3}{4}π±\displaystyle\frac{π}{3})\)

\(\tan(\displaystyle\frac{3}{4}π+\displaystyle\frac{π}{3})\)

\(=\displaystyle\frac{-1+\sqrt{3}}{1-(-1)\cdot\sqrt{3}}\)

\(=\displaystyle\frac{(-1+\sqrt{3})^2}{(1+\sqrt{3})(-1+\sqrt{3})}\)

\(=2-\sqrt{3}\)

\(\tan(\displaystyle\frac{3}{4}π-\displaystyle\frac{π}{3})\)

\(=\displaystyle\frac{-1-\sqrt{3}}{1+(-1)\cdot\sqrt{3}}\)

\(=\displaystyle\frac{(-1-\sqrt{3})(1+\sqrt{3})}{(1-\sqrt{3})(1+\sqrt{3})}\)

\(=\displaystyle\frac{(1+\sqrt{3})^2}{2}\)

\(=2+\sqrt{3}\)

したがって求める傾きは
\(2±\sqrt{3}\)

・2直線のなす角(鋭角)

(証明)
①②のなす角は、①②の交点が原点にくるように平行移動した
\(y=m_1x\)・・・①’,　\(y=m_2x\)・・・②’
のなす角である。

①’,②’と\(x\)軸の正の向きとなす角を\(α,β\) (\(0≦α<π\), \(0≦β<π\))とすると、
\(\tanα=m_1\),　\(\tanβ=m_2\)
垂直に交わらないので、\(m_1m_2≠-1\), 　\(α-β≠\displaystyle\frac{π}{2}\)\(,-\displaystyle\frac{π}{2}\)

以下①’②’のなす鋭角\(θ\)の正接について検討していく。

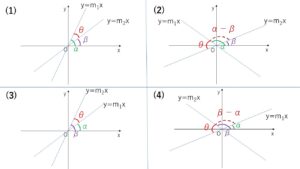
(ア)\(α-β>0\) について
\(0<α-β<π\) となり

(1)\(α-β\)が鋭角のとき
\(θ=α-β\) だから
\(\tanθ\)\(=\tan(α-β)\)\(=\displaystyle\frac{m_1-m_2}{1+m_1m_2}\)\((>0)\)

(2)\(α-β\)が鈍角のとき
\(θ=π-(α-β)\) だから
\(\tanθ\)\(=\tan\{π-(α-β)\}\)\(=-\tan(α-β)\)\(=-\displaystyle\frac{m_1-m_2}{1+m_1m_2}\)\((>0)\)

(イ)\(β-α>0\) について
\(0<β-α<π\) となり

(3)\(β-α\)が鋭角のとき
\(θ=β-α\) だから
\(\tanθ\)\(=\tan(β-α)\)\(=-\tan(α-β)\)\(=-\displaystyle\frac{m_1-m_2}{1+m_1m_2}\)\((>0)\)

(4)\(β-α\)が鈍角のとき
\(θ=π-(β-α)\) だから
\(\tanθ\)\(=\tan\{π-(β-α)\}\)\(=-\tan(β-α)\)\(=\tan(α-β)\)\(=\displaystyle\frac{m_1-m_2}{1+m_1m_2}\)\((>0)\)

以上より
\(\displaystyle\frac{m_1-m_2}{1+m_1m_2}\)\(=T\) とおくと

\(T>0\)のときは(1)(4)より、\(\tanθ=T\)
\(T<0\)のときは(2)(3)より、\(\tanθ=-T\)

したがって \(\tanθ\)\(=|T|\)\(=|\displaystyle\frac{m_1-m_2}{1+m_1m_2}|\)

最後にこの公式を利用して例題を解いてみます。

(1)
2直線 \(3x-y+1=0\),  \(x-2y+4=0\) のなす角\(θ\) (\(0°≦θ≦90°\) について

\(m_1=3\), \(m_2=\displaystyle\frac{1}{2}\) として

\(\tanθ=|\displaystyle\frac{3-\displaystyle\frac{1}{2}}{1+3\cdot\displaystyle\frac{1}{2}}|\)\(=|1|=1\)

よって \(θ=45°\)

(2)
直線 \(x=k\) は条件を満たさない。

\(y=-x+3\) と\(\displaystyle\frac{π}{3}\) の角をなす直線の傾きを\(m\)とする。
\(y=-x\) と \(y=mx\) のなす角が \(\displaystyle\frac{π}{3}\) だから、\(m_1=-1\), \(m_2=m\) として

\(\tan\displaystyle\frac{π}{3}\)\(=|\displaystyle\frac{-1-m}{1+(-1)\cdot m}|\)

\(\sqrt{3}\)\(=|\displaystyle\frac{m+1}{m-1}|\)

\(\sqrt{3}|m-1|=|m+1|\)

\(3(m-1)^2=(m+1)^2\)

\(m^2-4m+1=0\)

よって
\(m=2±\sqrt{3}\)

以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→2倍角・半角の公式　back→加法定理③