引き続き積和・和積の公式を利用する問題について見ていきます。
(例題1)\(△ABC\)の内角を\(A,B,C\)とするとき、次の等式を証明せよ。
(1)\(\sin A+\sin B+\sin C\)\(=4\cos\displaystyle\frac{A}{2}\)\(\cos\displaystyle\frac{B}{2}\)\(\cos\displaystyle\frac{C}{2}\)
(2)\(\cos A+\cos B+\cos C\)\(=4\sin\displaystyle\frac{A}{2}\)\(\sin\displaystyle\frac{B}{2}\)\(\sin\displaystyle\frac{C}{2}+1\)
(3)\(\tan A+\tan B+\tan C\)\(=\tan A\)\(\tan B\)\(\tan C\) (ただし\(A,B,C\)は\(\displaystyle\frac{π}{2}\)でないとする)
三角形の内角なので、\(A+B+C=π\) が成り立つのでこれを使って式変形してきます。
(解答)
(1)
\(A+B+C=π\) だから
\(\sin A+\sin B+\sin C\)
\(=\sin A+\sin B+\sin(π-(A+B))\)
\(=\sin A+\sin B+\sin(A+B)\)
(右辺が半角になっていることを意識して変形します)
\(=\)\(\sin A+\sin B\)\(+\sin(2×\displaystyle\frac{A+B}{2})\)
(青部分は和積、緑部分は2倍角の公式を利用して)
\(=\)\(2\sin\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A-B}{2}\)\(+2\sin\displaystyle\frac{A+B}{2}\)\(\cos\displaystyle\frac{A+B}{2}\)
\(=2\sin\displaystyle\frac{A+B}{2}(\cos\displaystyle\frac{A-B}{2}\)\(+\cos\displaystyle\frac{A+B}{2})\)
(再び和積の公式を利用して)
\(=2\sin\displaystyle\frac{A+B}{2}(2\cos\displaystyle\frac{A}{2}\cos\displaystyle\frac{-B}{2})\)
\(=2\sin(\displaystyle\frac{π}{2}-\displaystyle\frac{C}{2})\)\((2\cos\displaystyle\frac{A}{2}\cos\displaystyle\frac{B}{2})\)
\(=4\cos\displaystyle\frac{C}{2}\cos\displaystyle\frac{A}{2}\cos\displaystyle\frac{B}{2}\)
\(=\)(右辺)
(2)
((1)と似たような変形になります。)
\(\cos A+\cos B+\cos C\)
\(=\cos A+\cos B+\cos(π-(A+B))\)
\(=\cos A+\cos B-\cos(A+B)\)
(和積と半角の公式を利用して)
\(=2\cos\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A-B}{2}\)\(-(2\cos^2\displaystyle\frac{A+B}{2}-1)\)
\(=2\cos\displaystyle\frac{A+B}{2}\)\((\cos\displaystyle\frac{A-B}{2}-\cos\displaystyle\frac{A+B}{2})\)\(+1\)
(再び和積の公式を利用して)
\(=2\cos\displaystyle\frac{A+B}{2}\)\((-2\sin\displaystyle\frac{A}{2}\sin\displaystyle\frac{-B}{2})\)\(+1\)
\(=2\cos(\displaystyle\frac{π}{2}-\displaystyle\frac{C}{2})\)\((2\sin\displaystyle\frac{A}{2}\sin\displaystyle\frac{B}{2})\)\(+1\)
\(=4\sin\displaystyle\frac{C}{2}\)\(\sin\displaystyle\frac{A}{2}\sin\displaystyle\frac{B}{2}\)\(+1\)
\(=\)(右辺)
(3)
\(A+B+C=π\) より、左辺右辺とも\(C\)を消去して変形しても示せますが、解答ではもう少しすっきりとした解法にしてみます。
\(\tan C\)
\(=\tan(π-(A+B))\)
\(=-\tan(A+B)\)
\(=-\displaystyle\frac{\tan A+\tan B}{1-\tan A\tan B}\)
よって
\(\tan C\)\(=-\displaystyle\frac{\tan A+\tan B}{1-\tan A\tan B}\)
が成り立つので、分母を払って
\(\tan C(1-\tan A\tan B)\)\(=-(\tan A+\tan B)\)
整理すると
\(\tan A+\tan B+\tan C\)\(=\tan A\tan B\tan C\)
解き方も同じです。
(例題2)
(1)\(\sin A+\sin B\) を積の形で表せ。
(2)凸四角形\(ABCD\)の4つの内角を\(A,B,C,D\)で表すとき
\(\sin A+\sin B\)\(=\sin C+\sin D\)
が成り立つ四角形の形状を述べよ。
(解答)
(1)
和積の公式より
\(\sin A+\sin B\)
\(=2\sin\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A-B}{2}\)
(2)
また四角形\(ABCD\)ですから、\(A+B+C+D=2π\) が成り立つのでこれを利用して与式を変形していきます。
なお、凸(とつ)四角形とはへこんでいない四隅が尖がっている四角形です。(へこんでいる四角形は凹(おう)四角形といい、ブーメランのような形をしています) 正確にいうと凸四角形はすべての内角が\(180°\)を超えない四角形で、凹四角形は\(180°\)を超える内角をもつ四角形です。
条件より
\(A+B+C+D=2π\)
\(0<A<π\), \(0<B<π\), \(0<C<π\), \(0<D<π\)
与式から
\(2\sin\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A-B}{2}\)\(=2\sin\displaystyle\frac{C+D}{2}\cos\displaystyle\frac{C-D}{2}\)
\(C+D=2π-(A+B)\)より
\(\sin\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A-B}{2}\)\(=\sin(π-\displaystyle\frac{A+B}{2})\cos\displaystyle\frac{C-D}{2}\)
よって
\(\sin\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{A-B}{2}\)\(=\sin\displaystyle\frac{A+B}{2}\cos\displaystyle\frac{C-D}{2}\)・・・①
ここで、\(0<A<π\), \(0<B<π\) より
\(0<\displaystyle\frac{A+B}{2}<π\) だから、\(\sin\displaystyle\frac{A+B}{2}≠0\)
したがって①の両辺を\(\sin\displaystyle\frac{A+B}{2}\) で割って左辺に寄せると
\(\cos\displaystyle\frac{A-B}{2}-\cos\displaystyle\frac{C-D}{2}=0\)
和積の公式より
\(-2\sin\displaystyle\frac{A-B+C-D}{4}\)\(\sin\displaystyle\frac{A-B-C+D}{4}\)\(=0\)
よって
\(\sin\displaystyle\frac{A+C-(B+D)}{4}\)\(\sin\displaystyle\frac{A+D-(B+C)}{4}\)\(=0\)・・・②
条件から\(\sin\)の中身の範囲を調べてみて具体的な値を探ります。
ここで、\(0<A+C<2π\), \(0<B+D<2π\) より
\(-2π<A+C-(B+D)<2π\) だから
\(-\displaystyle\frac{π}{2}<\displaystyle\frac{A+C-(B+D)}{4}<\displaystyle\frac{π}{2}\)
同様に
\(-\displaystyle\frac{π}{2}<\displaystyle\frac{A+D-(B+C)}{4}<\displaystyle\frac{π}{2}\)
ゆえに②より
\(\displaystyle\frac{A+C-(B+D)}{4}=0\)
または
\(\displaystyle\frac{A+D-(B+C)}{4}=0\)
したがって
\(A+C=B+D\) または \(A+D=B+C\)
\(A+B+C+D=2π\) も合わせると
\(A+C=B+D=π\) または \(A+D=B+C=π\)
1つ目は対角の和が\(180°\) なので円に内接する四角形となり、
2つ目は、同じ側の内角の和が\(180°\) なので、\(AB/\!/CD\) の台形となります。
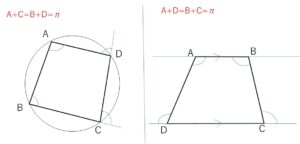
以上より
四角形\(ABCD\)は
円に内接する四角形 または \(AB/\!/CD\) の台形
まずは和積・積和の公式は文字通り、三角関数の和と積の変換に関する公式です。証明問題において左辺と右辺が和と積になっている場合などは和積・積和の利用が有力となります。また、和よりも積のほうが考えやすい場合、例えば方程式を解くような場合は、(積の形)\(=0\)のように変形するのが最終目標なので和積を使い、三角関数の積分(数Ⅲ)では和の形のほうが積分しやすいので積和を使ったりします。
あと積和・和積を使うと角の部分が和と差の形になるので、角の和や差が\(A+B=60°\) のように具体的に分かっているときや、\(A+B+C=180°\)のように和や差に関する等式がある場合などにも有効なことが多いです。
ただ、ある程度は慣れの部分もあるかと思います。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。