対称式である三角関数の最大最小問題について見ていきます。
(例題)1
\(0°≦θ<360°\) での
\((1+\sinθ)(1+\cosθ)\) の最大値、最小値を求めよ。
(解答)
\((1+\sinθ)(1+\cosθ)\)
\(=1+(\sinθ+\cosθ)+\sinθ\cosθ\)・・・①
そこで、先ほども書きましたが、①は\(\sinθ\)と\(\cosθ\)を入れ替えても変わらないので対称式となっていることに着目します。対称式は基本対称式である、
\(\sinθ+\cosθ\) ,\(\sinθ\cosθ\)
の2つの式を使って表すことができ、\(\sinθ+\cosθ\)のほうを別の文字\(t\)とおくと、\(t^2\)と\(\sin^2θ+\cos^2θ=1\) によりもう一方の\(\sinθ\cosθ\) を\(t\)を用いて表すことができます。あとは置き換えたので\(t\)の範囲に注意します。
ちなみに、\(\sinθ\cosθ\)のほうを最初に\(t\)でおくと、\(\sinθ+\cosθ\)は平方根の形で表されるので避けた方がよいです。
ここで、
\(\sinθ+\cosθ=t\) とおくと
合成して
\(t=\sqrt{2}\sin(θ+45°)\) と、\(0°≦θ<360°\) より
\(-\sqrt{2}≦t≦\sqrt{2}\)・・・②
また
\(t^2=\sin^2θ+\cos^2θ+2\sinθ\cosθ\) より
\(\sinθ\cosθ=\displaystyle\frac{1}{2}(t^2-1)\)
よって
\(1+(\sinθ+\cosθ)+\sinθ\cosθ\)
\(=\displaystyle\frac{1}{2}t^2+t+\displaystyle\frac{1}{2}\)
\(=\displaystyle\frac{1}{2}(t+1)^2\)
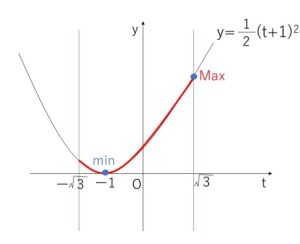
②の範囲から
最大値 \(t=\sqrt{2}\) のとき \(\displaystyle\frac{3+2\sqrt{2}}{2}\)
このとき\(θ\)の値を求めると
\(\sqrt{2}=\sqrt{2}\sin(θ+45°)\)
\(45°≦θ+45°<405°\) だから
\(θ+45°=90°\)
\(θ=45°\)
最小値 \(t=-1\) のとき \(0\)
このとき\(θ\)の値は
\(-1=\sqrt{2}\sin(θ+45°)\)
\(45°≦θ+45°<405°\) だから
\(θ+45°=225°,315°\)
\(θ=180°,270°\)
今回は練習のため指定の無いものを選びました。
(例題2)
実数\(a\)に対して、
\(y=2\sinθ\cosθ+a(\sinθ-\cosθ)\)
とする。
(1)\(x=\sinθ-\cosθ\) とおくとき、\(y\)を\(x\)で表せ。
(2)\(x\)のとりうる値の範囲を求めよ。
(3)\(y\)の最大値を\(a\)の式で表せ。
(解答)
(1)
\(x^2=\sin^2θ+\cos^2θ-2\sinθ\cosθ\) より
\(2\sinθ\cosθ=1-x^2\)
よって
\(y=1-x^2+ax\)
\(=-x^2+ax+1\)
(2)
合成すると
\(x\)\(=\sinθ-\cosθ\)
\(=\sqrt{2}\sin(θ-45°)\)
\(θ\)の範囲に制限がないので
\(-\sqrt{2}≦x≦\sqrt{2}\)
(3)
\(y\)\(=-x^2+ax+1\)
\(=-(x-\displaystyle\frac{a}{2})^2+\displaystyle\frac{a^2}{4}+1\)
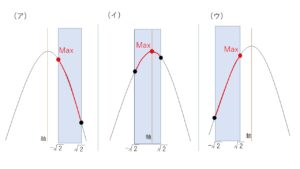
軸は \(x=\displaystyle\frac{a}{2}\) なので
(ア)
\(\displaystyle\frac{a}{2}<-\sqrt{2}\) (\(a<-2\sqrt{2}\)) のとき
最大値は \(x=-\sqrt{2}\) のとき
\(y=-x^2+ax+1\)
\(=-2-\sqrt{2}a+1\)
\(=-\sqrt{2}a-1\)
(イ)
\(-\sqrt{2}≦\displaystyle\frac{a}{2}≦\sqrt{2}\) (\(-2\sqrt{2}≦a≦2\sqrt{2}\)) のとき
最大値は \(x=\displaystyle\frac{a}{2}\) のとき
\(y=-(\displaystyle\frac{a}{2}-\displaystyle\frac{a}{2})^2+\displaystyle\frac{a^2}{4}+1\)
\(=\displaystyle\frac{a^2}{4}+1\)
(ウ)
\(\displaystyle\frac{a}{2}>\sqrt{2}\) (\(a>2\sqrt{2}\)) のとき
最大値は \(x=\sqrt{2}\) のとき
\(y=-x^2+ax+1\)
\(=-2+\sqrt{2}a+1\)
\(=\sqrt{2}a-1\)
以上をまとめると最大値は
\(-\sqrt{2}a-1\) (\(a<-2\sqrt{2}\))
\(\displaystyle\frac{a^2}{4}+1\) (\(-2\sqrt{2}≦a≦2\sqrt{2}\))
\(\sqrt{2}a-1\) (\(a>2\sqrt{2}\))
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→円の媒介変数表示 back→三角関数の最大最小③(合成型)