円上の点を\(θ\)を用いて表す方法について見ていきます。
(例題1)
実数\(x,y\) が、\(x^2+y^2=1\) を満たすとき、
\(3x^2+2xy+y^2\)
の最大値と最小値を求めよ。
1文字消去はうまくいきませんし、\(3x^2+2xy+y^2=k\) とおいて2次方程式の解の存在条件にもちこむこともできません。よって別の方法をとることになりますが、
\(x^2+y^2=1\) が原点中心の半径\(1\)の円(単位円)であることに着目すると、三角関数の定義から
\(x=\cosθ\), \(y=\sinθ\) とおくことができ、与式を\(θ\)のみの関数で表すことに成功します。2変数を、\(θ\)1つの変数にすることがポイントです。
(※一般的な円については下記参照)
(解答)
\(x^2+y^2=1\) は原点中心の半径1の円を表すから
\(x=\cosθ\), \(y=\sinθ\) (\(0≦θ<2π\)) とおける。
\(3x^2+2xy+y^2\)
\(=3\cos^2θ+2\cosθ\sinθ+\sin^2θ\)
\(=3\cdot\displaystyle\frac{1+\cos2θ}{2}+\sin2θ+\displaystyle\frac{1-\cos2θ}{2}\)
\(=\sin2θ+\cos2θ+2\)
\(=\sqrt{2}\sin(2θ+\displaystyle\frac{π}{4})+2\)
\(\displaystyle\frac{π}{4}≦2θ+\displaystyle\frac{π}{4}<\displaystyle\frac{17π}{4}\) (2周分)より
最大値 \(\sqrt{2}+2\)
最小値 \(-\sqrt{2}+2\)
ちなみに最大値のときをやっておくと、
\(1=\sin(2θ+\displaystyle\frac{π}{4})\) より、
\(2θ+\displaystyle\frac{π}{4}=\displaystyle\frac{π}{2},\displaystyle\frac{5π}{2}\)
よって \(θ=\displaystyle\frac{π}{8},\displaystyle\frac{9π}{8}\)
となるので、
\((x,y)=(\cos\displaystyle\frac{π}{8},\sin\displaystyle\frac{π}{8}),(\cos\displaystyle\frac{9π}{8},\sin\displaystyle\frac{9π}{8})\)
となります(半角の公式を使えば具体的な値にもなります)。最小値のときも同様に2組でてきます。
・円の媒介変数表示
例題1でも扱いましたが、
原点を中心とする半径\(1\)の円(単位円)上の点は、三角関数の定義から
\(x=\cosθ\), \(y=\sinθ\) \((0≦θ<2π)\) で表されます。
これを原点について\(r\)倍拡大(縮小)した図を考えると、
原点を中心とする半径\(r\)の円上の点は、
\(x=r\cosθ\), \(y=r\sinθ\) (\(0≦θ<2π\))
で表されることになります。
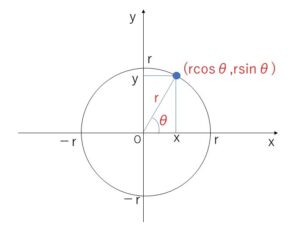
\(x,y\)ともに、変数\(θ\)を使って表しているので(変数\(θ\)で媒介されているので)、
この円の表示方法を、媒介変数表示とよびます。
また、中心\((a,b)\)の半径\(r\)の円については、\((a,b)\)が原点にくるように平行移動すると、原点中心の半径\(r\)の円に帰着できます。
移動前の円上の点を\((x,y)\)とすれば
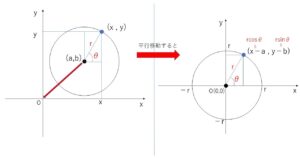
\(x-a=r\cosθ\)
\(y-a=r\sinθ\)
であるから、
\(x=r\cosθ+a\)・・・①
\(y=r\sinθ+b\)・・・② \((0≦θ<2π)\)
と表されることになります。
(例題2)
\(θ\)に関する方程式
\(\sinθ-k\cosθ=2(1-k)\)
が、\(-\displaystyle\frac{π}{2}≦θ≦\displaystyle\frac{π}{2}\) の範囲に解をもつように定数\(k\)の値の範囲を定めよ。
少々説明が長くなりますが、ご容赦ください。
\(\sin(θ+α)=k\)・・・(※)
という方程式の場合、\(θ\)に制限がない場合には\(\sin\)は最小値\(-1\)から最大値\(1\)の間しか動かないので、\(-1≦k≦1\) が解\(θ\)をもつ\(k\)の条件になります。
しかし本問では\(θ\)に制限がありますし、さらに\(k\)という文字が係数なので、\(α\)も\(k\)の値によって動き、最小値や最大値やそのときの\(θ\)が\(k\)によって変化します。なのでかなり面倒になりそうなので却下します。
\(x^2+y^2=1\)・・・①
\(y-kx=2(1-k)\)・・・② (与式より)
の2式が成り立ちます。問題の聞いていることは\(-\displaystyle\frac{π}{2}≦θ≦\displaystyle\frac{π}{2}\) の範囲に解\(θ\)をもつ\(k\)の条件、つまり①②を満たす\(x,y\)が第1象限か第4象限(軸上も含む)に存在すれば、題意を満たす\(θ\)が存在するので、そのような\(k\)の条件を求めればよいことになります。
なお解法としては、円①と直線②が交点をもつときを図示して考えるか、②を①に代入して1文字消去して2次方程式の解の存在条件を考えるかになりますが、前者のほうが計算は楽です。
\(\sinθ-k\cosθ=2(1-k)\) より \(k=\)の形(定数分離)にすると
\(k=\displaystyle\frac{\sinθ-2}{\cosθ-2}\)・・・③
③の右辺を\(f(θ)\)とおいて微分(数Ⅲ)して解いてもよいですし、
③は単位円右側の点と、定点\((2,2)\)を結ぶ直線の傾きを表しているので、その傾きの最小値と最大値を探す解き方をしてもよいです。
色々長くなりましたが、解答例では円と直線を図示して共有点をもつ条件を考える方法にしたいと思います。
(解答)
\(x=\cosθ\), \(y=\sinθ\) とおくと、\(-\displaystyle\frac{π}{2}≦θ≦\displaystyle\frac{π}{2}\) より
\(x^2+y^2=1\)・・・① (ただし \(0≦x≦1)\)
また与えられた方程式は
\(y-kx=2(1-k)\)・・・②
となるので、\(x,y\)の連立方程式①②が \(0≦x≦1\) の範囲で解をもつような\(k\)の条件を考えればよい。
②は \(y=k(x-2)+2\)・・・③ で 定点\((2,2)\)を通るので
①③を\(xy\)平面に図示することにより共有点をもつ\(k\)の範囲を求める。
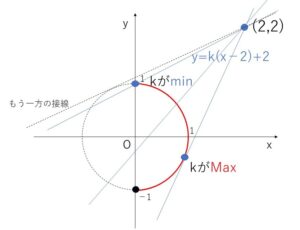
図より最小の\(k\)は直線③が \((0,1)\)を通るときだから③に代入して
\(1=k(0-2)+2\)
\(k=\displaystyle\frac{1}{2}\)
また最大の\(k\)は直線③と円が第4象限で接するときで、円の中心(原点)と直線の距離を考えると
\(\displaystyle\frac{|2(1-k)|}{\sqrt{k^2+1}}\)\(=1\)
両辺2乗して整理すると
\(3k^2-8k+3=0\)
\(k=\displaystyle\frac{4±\sqrt{7}}{3}\)
このうち第4象限で接するのは傾きが大きい方だから(小さい方は第2象限で接する)
\(k=\displaystyle\frac{4+\sqrt{7}}{3}\)
\(k\)が求めた最小値と最大値の間の値のときも円と直線③は共有点をもつので、\(k\)の範囲は
\(\displaystyle\frac{1}{2}≦k≦\displaystyle\frac{4+\sqrt{7}}{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角方程式の解の個数 back→三角関数の最大最小④(対称式型)