前回の復習です。
・整式の除法
同じ1つの文字についての(例えば\(x\)など)、2つの整式\(A,B\)において、\(A\)を\(B\)で割ったときの商を\(Q\)、余りを\(R\)とすると、
\(A=BQ+R\) (\(R\)の次数\(<B\)の次数) (\(B≠0\))
特に余りが\(0\)のとき、つまり\(R=0\)のときは「\(A\)は\(B\)で割り切れる」。
\(A=BQ+R\) がポイントとなる問題について見ていきます。
(例題1)
\(2x^2-2x+1\)で割ると、商が\(3x+2\)、余りが\(x+1\)である整式\(A\)を求めよ。
\(A=BQ+R\)で、
\(B=2x^2-2x+1\), \(Q=3x+2\), \(R=x+1\)
です。
\(B=2x^2-2x+1\), \(Q=3x+2\), \(R=x+1\)
です。
条件より
\(A=(2x^2-2x+1)(3x+2)+x+1\)
よって
\(A=6x^3-2x^2+3\)
(例題2)
整式\(2x^3+5x^2+4\)を整式\(P\)で割ると、商が\(2x+1\)で余りが\(-6x+2\)である。整式\(P\)を求めよ。
例題1と同様に等式をたてます。
(解答)
条件より
\(2x^3+5x^2+4\)\(=P(2x+1)-6x+2\)
よって
\(2x^3+5x^2+6x+2\)\(=(2x+1)P\)・・・①
①は \(2x^3+5x^2+6x+2\) が \(2x+1\) で割り切れて、その商が\(P\)であることを表している。
したがって、
\(P\)
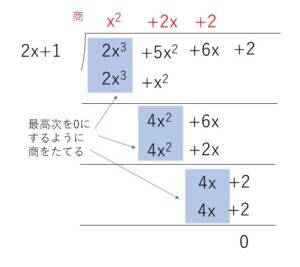
\(=(2x^3+5x^2+6x+2)\)\(÷(2x+1)\)
\(=\)\(x^2+2x+2\)
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。