本題に入る前に、素因数分解に関する用語の整理をしておきます。
・素因数、素因数分解
整数 \(297\)が、\(297=27×11\) のように整数の積で表されるとき、積を作る1つ1つの整数を、因数といい、とくに素数の因数を素因数といいます。\(27\)と\(11\)は\(297\)の因数であり、\(27\)は素因数ではなく、\(11\)は素因数です。
また、\(27\)を素数の積で表すと、\(27=3^3\) なので
\(297=3^3×11\)
と素因数の積で表すことができます。このように自然数を素数だけの積で表すことを素因数分解するといいます。
・階乗と素因数
次の問題について考えます。
\(10!\)を素因数分解したとき、\(2\)は何回掛けられているか。
\(10!\)くらいなら、具体的に書き出して数えることができますが、より一般的な場合でも解けるように次のように考えます。
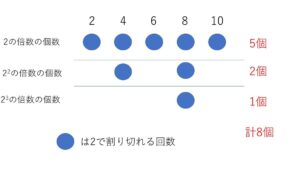
①まず、2の倍数が1~10のなかに何個あるかを数えます。2,4,6,8,10の5個
②①の2,4,6,8,10の中にはさらに2で割り切れるものがあります(2で2回割りきれる)。それは\(2^2\)の倍数である、4と8です。2個
③②の4,8の中には、さらに2で割り切れるものがあります(2で3回割り切れる)。それは\(2^3\)の倍数である、8です。1個
③②の4,8の中には、さらに2で割り切れるものがあります(2で3回割り切れる)。それは\(2^3\)の倍数である、8です。1個
④③の8はさらに2で割り切れません(2で4回割り切れるものはない)。\(2^4\)の倍数はないので、ここで終了です。
①~④から、\(10!\)が2で 5+2+1=8 (回) 割り切れることが分かったので、答えは8回となります。
これらを図にすると次の通りです。
\(p\)が何回掛けられているかを数えるには、
①\(p\)の倍数の個数 ②\(p^2\)の倍数の個数 ③\(p^3\)の倍数の個数・・・・
と数えていけばよいということです。
①\(p\)の倍数の個数 ②\(p^2\)の倍数の個数 ③\(p^3\)の倍数の個数・・・・
と数えていけばよいということです。
(例題)
\(30\)の階乗\(30!\)について、以下の問いに答えよ。
(1)\(2^k\)が\(30!\)を割りきるような最大の自然数\(k\)を求めよ。
(2)\(30!\)を計算すると、末尾に\(0\)が連続して何個並ぶか。
\(30\)の階乗\(30!\)について、以下の問いに答えよ。
(1)\(2^k\)が\(30!\)を割りきるような最大の自然数\(k\)を求めよ。
(2)\(30!\)を計算すると、末尾に\(0\)が連続して何個並ぶか。
(解答)
(1)
\(2\)で最大何回割り切れるか、つまり\(2\)が何回掛けられているかということです。
\(30\)までの数のうち、\(2^2\)の倍数の個数を数えるには、\(30÷2^2=7.5\) と計算をします。\(2^2×1,2^2×2\)\(・・・2^2×7\) の\(7\)個 (\(7.5\)の整数部分) が該当する個数となります。
\(30\)までの数のうち、\(2^2\)の倍数の個数を数えるには、\(30÷2^2=7.5\) と計算をします。\(2^2×1,2^2×2\)\(・・・2^2×7\) の\(7\)個 (\(7.5\)の整数部分) が該当する個数となります。
\(30!\)の素因数分解したときに、掛けられている\(2\)の個数を調べる。
\(1~30\)までの整数のうち
①\(2\)の倍数の個数は、\(30÷2=15\) より、\(15\) 個
②\(2^2\)の倍数の個数は、\(30÷2^2=7.5\) より、\(7\) 個
③\(2^3\)の倍数の個数は、\(30÷2^3=3.75\) より、\(3\) 個
④\(2^4\)の倍数の個数は、\(30÷2^4=1.875\) より、\(1\) 個
②\(2^2\)の倍数の個数は、\(30÷2^2=7.5\) より、\(7\) 個
③\(2^3\)の倍数の個数は、\(30÷2^3=3.75\) より、\(3\) 個
④\(2^4\)の倍数の個数は、\(30÷2^4=1.875\) より、\(1\) 個
⑤\(2^5=32\) より、\(2^5\)の倍数はない。
よって、\(2\)が \(15+7+3+1=26\) (回)掛けられているので、
\(k=26\)
\(k=26\)
(2)
\(10\)が何回掛けられているかを数えることになります。
\(10=2×5\) なので、\(2\)と\(5\)の掛けられている回数を数えるのですが、
\(1\)から順に数えると、\(2\)の倍数は\(2\)回に\(1\)回表れ、\(5\)の倍数は\(5\)回に\(1\)回表れるので、\(2\)の掛けられている回数の方が明らかに多いです(\(2^2\)と\(5^2\)の倍数・・・も同様)。
よって、\(5\)の掛けられている個数だけを調べればよいことになります。
\(10=2×5\) なので、\(2\)と\(5\)の掛けられている回数を数えるのですが、
\(1\)から順に数えると、\(2\)の倍数は\(2\)回に\(1\)回表れ、\(5\)の倍数は\(5\)回に\(1\)回表れるので、\(2\)の掛けられている回数の方が明らかに多いです(\(2^2\)と\(5^2\)の倍数・・・も同様)。
よって、\(5\)の掛けられている個数だけを調べればよいことになります。
\(30!\)の素因数分解したときに、掛けられている\(2\)の個数は\(5\)の個数より多いので、\(5\)の掛けられている個数を調べる。
\(1~30\)までの整数のうち
①\(5\)の倍数の個数は、\(30÷5=6\) より、\(6\) 個
②\(5^2\)の倍数の個数は、\(30÷5^2=1.2\) より、\(1\) 個
③\(5^3=75\)より、\(5^3\)の倍数はない。
②\(5^2\)の倍数の個数は、\(30÷5^2=1.2\) より、\(1\) 個
③\(5^3=75\)より、\(5^3\)の倍数はない。
よって、\(5\)の掛けられている個数は \(6+1=7\) (個) だから
連続して並ぶ\(0\)の数は \(7\)個
連続して並ぶ\(0\)の数は \(7\)個
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。