次の問題について考えてみましょう。
(例題)
\(n+7\) と \(n+1\) がともに \(n^2-7\) の整数倍となるような正の整数\(n\)をすべて求めよ。
問題文の条件を素直に式として表しても解くことができますが(別解参照)、
\(n\)に具体的に\(1,2,3・・・\)と代入してみて(実験してみて)、条件に適するものを探る方法を紹介します。難しい問題になるほど、この試しに代入してみるという方法が有効になることがあります。
\(n\)に具体的に\(1,2,3・・・\)と代入してみて(実験してみて)、条件に適するものを探る方法を紹介します。難しい問題になるほど、この試しに代入してみるという方法が有効になることがあります。
代入してみても分かりますが、\(n^2-7\) というのは2次式なので、\(n\)を大きくすると、\(n+7\) と \(n+1\) に比べてどんどん大きくなってしまうので、条件に合わなくなります。
\((n^2-7)-(n+7)=n(n-1)-14\) は、\(n=4\) のとき負、\(n=5\)のとき正の値なので、\(n≦4\) のときと、\(n≧5\) のときで場合わけします。
\((n^2-7)-(n+7)=n(n-1)-14\) は、\(n=4\) のとき負、\(n=5\)のとき正の値なので、\(n≦4\) のときと、\(n≧5\) のときで場合わけします。
(解答)
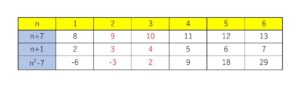
①\(1≦n≦4\) のとき
表より条件を満たすのは \(n=2,3\)
表より条件を満たすのは \(n=2,3\)
②\(n≧5\) のとき
\((n^2-7)-(n+7)=n(n-1)-14≧5・4-14>0\)
であり
\((n^2-7)-(n+1)>(n^2-7)-(n+7)>0\)
だから、\(n^2-7\) は、\(n+7\), \(n+1\) より大きい。
よって条件に合わず不適。
であり
\((n^2-7)-(n+1)>(n^2-7)-(n+7)>0\)
だから、\(n^2-7\) は、\(n+7\), \(n+1\) より大きい。
よって条件に合わず不適。
以上より
\(n=2,3\)
\(n=2,3\)
(別解)
条件より、整数\(k,l\)を用いて
\(n+7=k(n^2-7)\)・・・①
\(n+1=l(n^2-7)\)・・・②
\(n+7=k(n^2-7)\)・・・①
\(n+1=l(n^2-7)\)・・・②
とおける。
左辺の\(n\)を消去するイメージで①ー②をします。
すると、左辺が\(6\)、右辺が (整数)×(整数) の形になり、
因数分解型の整数問題になります。
すると、左辺が\(6\)、右辺が (整数)×(整数) の形になり、
因数分解型の整数問題になります。
①ー②より
\(6=(k-l)(n^2-7)\)・・・③
\(6=(k-l)(n^2-7)\)・・・③
\(k-l\),\(n^2-7\) は整数なので、掛けて\(6\)になる整数はかなり限られます。
その組み合わせは、
\((k-l,n^2-7)=\)\((±6,±1),(±1,±6)\)\((±2,±3),(±3,±2)\)
\(n^2-7\) がこれらの値になるときに、\(n\)が正の整数となるものを絞りましょう。
その組み合わせは、
\((k-l,n^2-7)=\)\((±6,±1),(±1,±6)\)\((±2,±3),(±3,±2)\)
\(n^2-7\) がこれらの値になるときに、\(n\)が正の整数となるものを絞りましょう。
ここで、\(6=(±6)×(±1),(±2)×(±1)\) (複号同順) なので
\(n^2-7=1,2,3,6,\)\(-1,-2,-3,-6\)
\(n^2-7=1,2,3,6,\)\(-1,-2,-3,-6\)
このうち\(n\)が正の整数となるのは
\(n^2-7=2,-3,-6\) のときで
\(n=1,2,3,\)
最後に\(n=1,2,3\) がちゃんと条件に合うか確かめます。(十分性の確認)
確かめる必要がある理由は
(1)\(k,l\) が整数になっているか分からない。(\(k,l\)が整数でなくても、\(k-l\)が整数となることはあります。2.5-1.5 など)
(2)③が成り立つからといって、①②が成り立つとは限らない
からです。(2)については仮に①②が
\(n+8=k(n^2-7)\)・・・①’
\(n+2=l(n^2-7)\)・・・②’
となっていても③が導かれるので、③ならば①かつ② とは必ずしもいえないことになります。
確かめる必要がある理由は
(1)\(k,l\) が整数になっているか分からない。(\(k,l\)が整数でなくても、\(k-l\)が整数となることはあります。2.5-1.5 など)
(2)③が成り立つからといって、①②が成り立つとは限らない
からです。(2)については仮に①②が
\(n+8=k(n^2-7)\)・・・①’
\(n+2=l(n^2-7)\)・・・②’
となっていても③が導かれるので、③ならば①かつ② とは必ずしもいえないことになります。
(ア)\(n=1\) のとき
①②より
\(8=k(-6)\), \(2=l(-6)\)
となり、\(k,l\)は整数でないため不適
①②より
\(8=k(-6)\), \(2=l(-6)\)
となり、\(k,l\)は整数でないため不適
(イ)\(n=2\) のとき
①②より
\(9=k(-3)\), \(3=l(-3)\)
となり、適する。
(ウ)\(n=3\) のとき
①②より
\(10=k・2\), \(4=l・2\)
となり、適する。
以上より、\(n=2,3\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。