まずは最小公倍数、最大公約数の定義から始めます。
・最小公倍数・最大公約数
2つ以上の整数について、それらの共通な約数を公約数といい、公約数のうち最大のものを最大公約数といいます。
また、2つ以上の整数について、それらに共通な倍数を公倍数といい、公倍数のうち正で最小のものを最小公倍数といいます。
(例)\(12\)と\(18\)の公約数について
\(12\)の約数:\(1,2,3\)\(,4,\)\(6\)\(,12\)
\(18\)の約数:\(1,2,3,6\)\(,9,18\)
正の公約数:\(1,2,3,6\) 最大公約数\(6\)
\(12\)と\(18\)の公倍数について
\(12\)の倍数:\(12,24,\)\(36\)\(,48,60,\)\(72\)\(,84,96,\)\(108\)\(,・・・\)
\(18\)の倍数:\(18,\)\(36\)\(,54,\)\(72\)\(,90,\)\(108\)\(,・・・\)
正の公倍数:\(36,72,108,・・・\) 最小公倍数\(36\)
・最小公倍数・最大公約数の性質
①上の例からも分かりますが、公約数は最大公約数の約数、公倍数は最小公倍数の倍数となります。(厳密には証明が必要です)
②2つの自然数\(A,B\)の最大公約数を\(g\)とすると
\(A=ag\), \(B=bg\) (\(a,b\)は自然数)と表すことができます。
このとき
(1)\(a,b\)の最大公約数は\(1\)となる。(互いに素であるともいう)
(例) \(12=6×2\), \(18=6×3\) \(2,3\)は互いに素。
(2)\(A,B\)の最小公倍数を\(l\)とすると、
\(l=gab=Ab=aB\)
(例) \(12=6×2\), \(18=6×3\) より
\(l=6×2×3=36\)
(3)
\(AB=gl\)
よって、2つの自然数の積は、2つの自然数の最小公倍数と最大公約数の積となります。
(例題1)
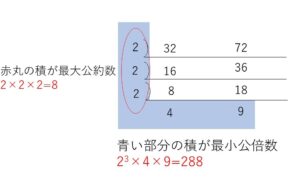
\(32\)と\(72\)の最小公倍数と最大公約数をそれぞれ求めよ。
(解答1)素因数分解を利用する方法
\(32=2^5\)
\(72=2^3×3^2\)
だから
\(32=2^3×2^2=8×4\)
\(72=2^3×3^2=8×9\)
よって、
最小公倍数は \(8×4×9=\)\(288\)
最大公約数は \(8\)
\(32\)と\(72\)を素因数分解したときに、各因数の最も次数が高いもの(\(2^5\)と\(3^2\))を掛けたものが最小公倍数となります。
\(32\)に□を掛けて、\(72\)に△を掛けて同じにするには、□は\(3^2\)で、
△は\(2^2\)だと最も数が小さくなります。できた数は、\(2^5×3^2\) であり、これは最も次数が高いものを掛けたものになっています。
なお、最大公約数は、各因数で次数が最も低いもの(\(2^3\)と\(3^0(=1)\))を掛けたものになります。
(解答2)共通な素因数で割っていく方法
(例題2)
3つの数、\(24,30,168\) の最大公約数と最小公倍数を求めよ。
(解答1)素因数分解を利用する方法
\(24=2^3×3\)
\(30=2×3×5\)
\(168=2^3×3×7\)
だから
\(24=2×3×2^2=6×4\)
\(30=2×3×5=6×5\)
\(168=2×3×2^2×7=6×28\)
よって、最大公約数は\(6\)
最小公倍数は、\(4,5,28(=4×7)\) の最小公倍数が \(4×5×7=140\) であるから
\(6×140=\)\(840\)
最小公倍数は、最も次数が高いものを選んで掛けると
\(2^3×3×5×7=840\)
最大公約数は、次数が低いものを選んで掛けると
\(2×3=6\)
(解答2)共通な素因数で割っていく方法

最大公約数は\(6\)
最小公倍数は\(840\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。