整数問題において、解く方針が見つからない場合には具体的に値を代入してみる(実験してみる)ことで、手がかりが見つかることがあります。
(例題)
\(p\),\(2p+1\),\(4p+1\) がいずれも素数であるような\(p\)をすべて求めよ。
ひとまず、素数\(p\)に具体的な値を代入してみて、何か手がかりがないか探ってみます。
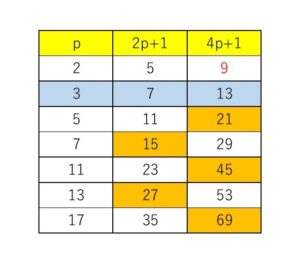
\(p=2\)のときは、\(4p+1=9\) なので不適で、
\(p=3\)のときは、すべて素数となっています。
\(p≧5\)のときは、\(2p+1\)と\(4p+1\)のどちらかが\(3\)の倍数となっているので、表にはない数でも\(3\)の倍数ではないかと予想します。
予想は証明する必要があります。\(3\)の倍数であることの証明なので、\(p\)を\(3\)で割った余りで分類します。ただし、\(p=3k\) (\(k≧2\) )の場合は\(p\)が\(3\)より大きい\(3\)の倍数で、素数ではないのでこれは除外します。
(解答)
\(p=2\) のとき \(4p+1=9\) より、素数ではないため不適。
\(p=3\) のとき \(2p+1=7\), \(4p+1=13\) より適する。
\(p≧5\) のとき、\(p\)は素数なので
\(p=3k+1\) (\(k≧2\)の整数)
\(p=3k+2\) (\(k≧1\)の整数)
とおける。
\(p=3k+1\) のとき、
\(2p+1=2(3k+1)+1=3(2k+1)\) であり、\(3\)より大きい\(3\)の倍数となり素数ではない。
\(p=3k+2\) のとき、
\(4p+1=4(3k+2)+1=3(4k+3)\) であり、\(3\)より大きい\(3\)の倍数となり素数ではない。
よって、\(p≧5\) のときは、\(2p+1\),\(4p+1\)のどちらかは素数ではない。
以上より \(p=3\)
\(3\)より大きい\(3\)の倍数という明記が必要となります。
以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。