不定方程式範囲で絞る型①

範囲をしぼって解く不定方程式について見ていきます。

まずは1次式からです。

(例題1)
\(x,y\)を自然数とするとき
(1)\(2x+3y=27\) を解け。
(2)\(3x+2y+z=11\) を解け。

どちらも\(x,y\)は自然数という条件がついています。
ざっくり見ても、(1)については\(y\)を\(1\)からどんどん大きくしていくと、\(y=9\) のときには左辺は27より大きいので\(8\)以下になりそうです。
これを数式で処理するには、\(3y=27-2x\) として、\(x\)に\(1\)を代入したときが右辺が最も大きくなるので、\(3y=27-2x≦27-2\) として不等式で表します。
\(2x=27-3y\) として、\(2x=27-3y≦27-3\) とやってもよいですが、係数が大きいほうの範囲を絞った方が場合分けが楽になります。

(1)
与式より
\(3y=27-2x≦27-2×1=25\) だから、
\(3y≦25\)
\(y≦\displaystyle\frac{25}{3}≒8.3\)
よって、\(1≦y≦8\)

この範囲の\(y\)全部を確かめてもよいですが、与式より \(x=\displaystyle\frac{27-3y}{2}\) なので、\(27-3y\) は偶数です。

ここで、\(2x=27-3y\)・・・① より、\(27-3y\)は偶数なので、
\(y=1,3,5,7\)

\(y=1\) のとき ①より \(2x=24\) だから、\(x=12\)
その他の\(y\)についても同様に求めると
\(y=3\) のとき \(x=9\)
\(y=5\) のとき \(x=6\)
\(y=7\) のとき \(x=3\)

以上より

\((x,y)=(3,7),(6,5)\)\(,(9,3),(12,1)\)

※なお1次不定方程式を解くと
\(2x=3(9-y)\) から
\(x=3k\), \(9-y=2k\) (\(k\)は整数) より
\(x=3k\), \(y=-2k+9\) ・・・(A) です。
\(x,y\) が自然数だから
\(3k>0\),\(-2k+9>0\) で
\(0<k<\displaystyle\frac{9}{2}\) より
\(k=1,2,3,4\) を(A)に代入すれば、自然数解がでます。

(格子点について)
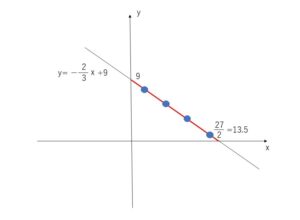
\(2x+3y=27\)・・・(B)を、\(x\)の1次関数とみると
\(y=-\displaystyle\frac{2}{3}x+9\) より、グラフは次の通り。
(B)を満たす\(x,y\)は、この直線上にあるすべての点の座標ですが、整数解と限定すると\(x,y\)がともに整数となる点の座標です(このような点を格子点といいます)。整数解という限定方法では、解が(A)なので無数にあることになりますが、自然数解とさらに限定すると、第1象限だけを考えればよいので、グラフの赤色の部分の格子点の座標が解となり有限です。

(2)
(1)と同様にして
\(3x=11-(2y+z)≦11-(2×1+1)=8\) より
\(3x≦8\)
\(x≦\displaystyle\frac{8}{3}≒2.6\)
\(x\)は自然数だから
\(1≦x≦2\)

(ア)\(x=1\)のとき与式は
\(2y+z=8\) ・・・①

①も不等式で\(y\)の範囲を絞ってもよいですが、簡単なので、\(y\)に\(1\)から順に自然数を代入していって\(y=4\) にはならないことを頭の中でやってしまいます。

①を満たす自然数\(y\)は \(y=1,2,3\) の場合で、このとき\(z\)はそれぞれ
\(z=6,4,2\)

(イ)\(x=2\) のとき与式は
\(2y+z=5\) ・・・②
②を満たす自然数\(y\)は \(y=1,2\) の場合で、このとき\(z\)はそれぞれ
\(z=3,1\)

以上より
\((x,y,z)=(1,1,6),(1,2,4)\)\(,(1,3,2),(2,1,3),(2,2,1)\)

続いて2次式です。

(例題2)
(1)\(b\)を正の整数とするとき、等式 \(6-b-2a-4a^2=0\) を満たす整数\(a,b\)の組をすべて求めよ。
(2)\(x^2+4y^2-2x-4y-23=0\) を満たす整数\(x,y\)の値を求めよ。

(解答)
(1)

\(b\)については1次式なので、\(b=・・・\) と表して、\(b>0\) から\(a\)の範囲を絞ります。

与式より
\(b=-4a^2-2a+6\)・・・①
\(b\)は正の整数だから
\(-4a^2-2a+6>0\)
\(2a^2+a-3<0\)
\((2a+3)(a-1)<0\) より
\(-\displaystyle\frac{3}{2}<a<1\)

\(a\)は整数だから、\(a=-1,0\)

\(a=-1\) のとき、①より \(b=4\)

\(a=0\) のとき、①より \(b=6\)

以上から
\((a,b)=(-1,4),(0,6)\)

(2)

\(x,y\) それぞれ平方完成します。
(・・・)\(^2\)は、\(0\)以上の値となることを利用します。

与式より\(x,y\)についてそれぞれ平方完成して
\((x-1)^2-1+(2y-1)^2-1-23=0\)
\((x-1)^2+(2y-1)^2=25\)・・・(C)

(C)式より、(・・・)\(^2\) は0以上の数なので、\((2y-1)^2\) が\(25\)以下であることはわかります。以下それを数式で表しています。

(係数が大きい\(y\)について範囲を絞ると)
\((x-1)^2=25-(2y-1)^2\)・・・② より、左辺は\(0\)以上実数だから
\(25-(2y-1)^2≧0\)
\((2y-1)^2≦25\)
\(2y-1\) は奇数だから
\(2y-1=±1,±3,±5\)

(ア)\(2y-1=±1\) のとき
②より　\((x-1)^2=24\) から \(x\)は整数ではないため不適

(イ)\(2y-1=±3\) のとき
②より　\((x-1)^2=16\) から \(x-1=±4\)
よって \(y=2\) のとき \(x=-3,5\)、 \(y=-1\) のとき \(x=-3,5\)

(ウ)\(2y-1=±5\) のとき
②より \((x-1)^2=0\) から \(x=1\) このとき \(y=3,-2\)

以上より
\((x,y)=(1,-2),(1,3),\)\((-3,-1),(5,-1)\)\(,(-3,2),(5,2)\)

なお(2)の別解については、→(4-10)2次不定方程式と判別式の例題1を参照してください。全く同じ問題です。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。

→高校数学TOP　next→不定方程式範囲で絞る型②　back→整数となる分数式