定積分で表された関数の極値に関する問題について見ていきます。
(例題1)
関数 \(f(x)=\displaystyle\int_{-2}^x(t^2+t-2)dt\) の極値と、それを与える\(x\)の値を求めよ。
(解答)
\(f(x)=\displaystyle\int_{-2}^x(t^2+t-2)dt\) より
\(f'(x)=x^2+x-2=(x+2)(x-1)\)
よって
極大値をとるとき \(x=-2\)
極小値をとるとき \(x=1\)
\(f(-2)=\displaystyle\int_{-2}^{-2}(t^2+t-2)dt\)\(=0\)
\(f(1)=\displaystyle\int_{-2}^1(t^2+t-2)dt\)
\(=\displaystyle\int_{-2}^1(t+2)(t-1)dt\) (1/6公式が使える)
\(=-\displaystyle\frac{1}{6}(1+2)^3\)
\(=-\displaystyle\frac{9}{2}\)
以上から
極大値 \(0\) (\(x=-2\))
極小値 \(-\displaystyle\frac{9}{2}\) (\(x=1\))
(例題2)
\(F(x)=\displaystyle\int_0^x(at^2+bt+c)dt\) で表される関数 \(F(x)\) は \(x=1\) で極小値 \(-4\) をとり、\(x=3\) でも極値をとるとする。このとき \(a,b,c\) の値を求めよ。
なお、\(x=1,3\)で極値をとることから導関数の符号が変わっていることの確認、特に\(x=1\)で極小値となっているから「負から正」に変わっていることのチェックをしておきます。
(解答)
\(F(x)=\displaystyle\int_0^x(at^2+bt+c)dt\) において
\(F'(x)=ax^2+bx+c\)
\(x=1,3\) で極値をとるから、これらが\(F'(x)=0\) の解になり
\(a+b+c=0\)・・・①
\(9a+3b+c=0\)・・・②
また \(x=1\) で極小値 \(-4\) をとるから
\(F(1)=-4\)
\(F(1)=\displaystyle\int_0^1(at^2+bt+c)dt\)
\(=\left[\displaystyle\frac{a}{3}t^3+\displaystyle\frac{b}{2}t^2+ct\right]_0^1\)
\(=\displaystyle\frac{a}{3}+\displaystyle\frac{b}{2}+c\)
よって
\(\displaystyle\frac{a}{3}+\displaystyle\frac{b}{2}+c=-4\)・・・③
①②③より\(a,b,c\)を求めると(途中式省略)
\(a=-3\), \(b=12\), \(c=-9\)
逆にこのとき
\(F'(x)=-3x^2+12x-9\)
\(=-3(x-1)(x-3)\)
であり、\(x=1,3\) で極値をとり、特に \(x=1\)で極小値をとるから題意を満たす。
(例題3)
\(-3≦x≦3\) のとき、関数 \(f(x)=\displaystyle\int_{-3}^{x}(t^2-2t-3)dt\) のとりうる値の範囲を求めよ。
最大値と最小値が知りたいので、極値と範囲の端点\(x=-3,3\)のときの値に注目です。今回は積分計算が複数必要なので、\(f(x)\)を積分して求めておきます。
(解答)
\(f(x)=\displaystyle\int_{-3}^{x}(t^2-2t-3)dt\) (\(-3≦x≦3\)) において
\(f'(x)=x^2-2x-3\)\(=(x+1)(x-3)\)
\(f'(x)=0\)となるのは \(x=-1,3\)
また
\(f(x)=\displaystyle\int_{-3}^{x}(t^2-2t-3)dt\)
\(=\left[\displaystyle\frac{1}{3}t^3-t^2-3t\right]_{-3}^x\)
\(=\displaystyle\frac{1}{3}x^3-x^2-3x+9\)
よって増減表は次の通り。
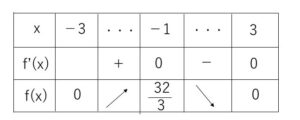
したがって
\(0≦f(x)≦\displaystyle\frac{32}{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→次数と定積分 back→定積分を含む関数②(定積分の微分)