定積分と面積の関係

面積と定積分の関係について見ていきます。

・定積分と面積

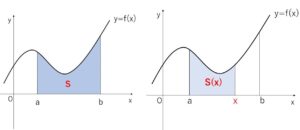
区間 \(a≦x≦b\) において \(f(x)≧0\) となる関数について
曲線 \(y=f(x)\) と \(x=a\), \(x=b\), \(x\)軸 で囲まれる図形の面積\(S\)がどのような式で表されるか考えます。

曲線 \(y=f(x)\) と \(x\)軸の間にある図形の、\(x\)座標が\(a\)から\(x\)までの部分の面積は、\(x\)を1つ決めると面積の値が1つ決まるので\(x\)の関数で表すことができ、それを\(S(x)\)とおきます。

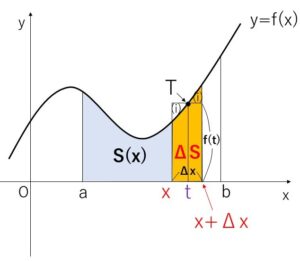
ここで、\(x\)の値が \(x\) から \(x+Δx\)  (\(Δx>0\)) で変化した場合の\(S(x)\)の変化量を

\(ΔS=S(x+Δx)-S(x)\)

とおくと、\(ΔS\)は曲線と\(x\)軸の間の図形の\(x\)から\(x+Δx\)までの部分の面積となり、この図形が「横の長さ\(Δx\), 縦の長さ\(f(t)\) の長方形」の面積に等しくなるように\(t\)をとります。(このとき図の2つの(i)の部分の面積が等しく、点\(T\)の\(x\)座標が\(t\)となる)

\(S(x+Δx)-S(x)=Δxf(t)\)

より両辺を\(Δx\)で割ると

\(\displaystyle\frac{S(x+Δx)-S(x)}{Δx}=f(t)\)

ここで、\(Δx\)を限りなく\(0\)に近づけると、\(t\)は限りなく\(x\)に近づくので

\(\displaystyle\lim_{Δx \to 0}\displaystyle\frac{S(x+Δx)-S(x)}{Δx}=f(x)\)・・・①

\(Δx<0\)のときも同様に①が成り立つので(このときは \(Δx\)も\(ΔS\)も負になる)

\(\displaystyle\frac{dS}{dx}=S'(x)=f(x)\)

つまり、\(S(x)\)は\(f(x)\)の不定積分の1つになります。

\(f(x)\)の任意の不定積分を\(F(x)\)とすると
\(S(x)=F(x)+C\)・・・②　(\(C\)は定数)
と表せて、\(S(x)\)の定義から \(S(a)=0\) となるので②で\(x=a\)を代入すると
\(0=F(a)+C\)
\(C=-F(a)\)

②より
\(S(x)=F(x)-F(a)\)

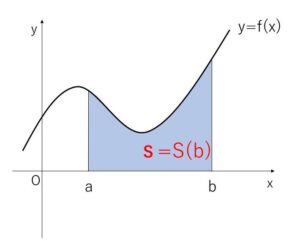
求める面積\(S\)は\(S(b)\) なので
\(S=S(b)=F(b)-F(a)=[F(x)]_a^b\)

したがって積分記号を用いて\(S\)は次のように表されます。

\(S=\displaystyle\int_a^bf(x)dx\)

・負の領域の面積
今度は負の領域の面積がどうなるかを考えます。

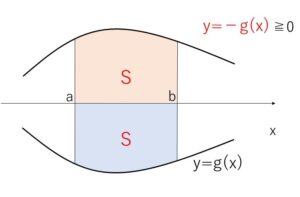
区間 \(a≦x≦b\) において \(g(x)≦0\) となる関数について
曲線 \(y=g(x)\) と \(x=a\), \(x=b\), \(x\)軸 で囲まれる図形の面積\(S\)は、\(y=g(x)\)を\(x\)軸について対称移動することで(折り返すことで)、正の領域の面積に帰着できます。

つまり、\(y=-g(x)\) は 区間 \(a≦x≦b\) において \(-g(x)≧0\) となるから

\(S=\displaystyle\int_a^b\{-g(x)\}dx=-\displaystyle\int_a^bg(x)dx\)

(\(-S=\displaystyle\int_a^bg(x)dx\)) 　(負の面積)

よって次のような図形の面積 \(S=S_1+S_2+S_3\) を求める場合には、負の部分を正として扱う、つまり絶対値をとればよいことになる。

\(S=S_1+S_2+S_3\)
\(=\displaystyle\int_a^cf(x)dx+\displaystyle\int_c^d\{-f(x)\}dx+\displaystyle\int_d^bf(x)dx\)
\(=\displaystyle\int_a^c|f(x)|dx+\displaystyle\int_c^d|f(x)|dx+\displaystyle\int_d^b|f(x)|dx\)
\(=\displaystyle\int_a^b|f(x)|dx\)

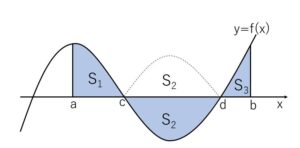
したがって一般的に
\(S=\displaystyle\int_a^b|f(x)|dx\)

なお、上図でそのまま \(\displaystyle\int_a^bf(x)dx\) を計算すると

\(\displaystyle\int_a^bf(x)dx\)
\(=\displaystyle\int_a^cf(x)dx+\displaystyle\int_c^df(x)dx+\displaystyle\int_d^bf(x)dx\)
\(=\displaystyle\int_a^cf(x)dx-\displaystyle\int_c^d\{-f(x)\}dx+\displaystyle\int_d^bf(x)dx\)
\(=S_1-S_2+S_3\)

と、正の領域の面積と負の領域の面積の差になる。

・2曲線間の面積

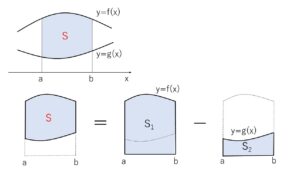
2つの曲線 \(y=f(x)\), \(y=g(x)\) が 区間\(a≦x≦b\) において
\(f(x)≧g(x)≧0\) の関係が成り立っているとします。

この2曲線と \(x=a\), \(x=b\) で囲まれた図形の面積\(S\)は、
「\(y=f(x)\) と \(x\)軸, \(x=a\), \(x=b\) で囲まれた図形の面積\(S_1\)」
「\(y=g(x)\) と \(x\)軸, \(x=a\), \(x=b\) で囲まれた図形の面積\(S_2\)」
を考えると

\(S=S_1-S_2\)
\(=\displaystyle\int_a^bf(x)dx-\displaystyle\int_a^bg(x)dx\)
\(=\displaystyle\int_a^b\{f(x)-g(x)\}dx\)

また、\(f(x)\)や\(g(x)\)が負の値をとることがある場合でも、\(f(x)≧g(x)\) の関係が成り立っていれば、\(y\)軸方向にどちらも\(0\)以上になるように平行移動すれば、上記の \(f(x)≧g(x)≧0\) に帰着できます。

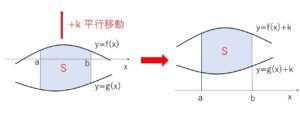
つまり、適当な正の定数\(k\)をとって
\(y=f(x)+k\), 　\(y=g(x)+k\) が、区間\(a≦x≦b\) で
\(f(x)+k≧g(x)+k≧0\) が成り立つようにすると、平行移動しても面積は変わらないので

\(S=\displaystyle\int_a^b\{f(x)+k-(g(x)+k)\}dx\)
\(=\displaystyle\int_a^b\{f(x)-g(x)\}dx\)

と全く同じ式なります。

なお、区間内で \(f(x)≦g(x)\) の部分があるときは、そこの部分の差を \(g(x)-f(x)\)\((≧0)\) に入れ替えて\(0\)以上の値になるようにすればよく、結局2曲線の囲む面積の場合でも絶対値を使って

\(S=\displaystyle\int_a^b|f(x)-g(x)|dx\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→面積の計算①(基礎)　back→積分方程式