面積の最大最小問題です。
「面積を求める→最大最小値を求める(微分するなど)」が基本的な流れです。
(例題1)
座標平面上に \(y=x^2-(t^2-t)\) と 直線 \(y=-x\) がある。ただし、\(t\)は定数とする。
\(0≦x≦1\) において、放物線 \(y=x^2-(t^2-t)\) と 直線 \(y=-x\) にはさまれた部分の面積を\(S\)とする。
(1)\(t≧1\) のとき、\(S\)を\(t\)で表せ。
(2)\(t≧1\) のとき、\(S\)の最小値を求めよ。
(解答)
(1)
まずは放物線の位置や、直線との位置関係を調べます。(交点などを求めていきます)
\(-(t^2-t)=-t(t-1)≦0\) (∵ \(t≧1\))
よって放物線の\(y\)切片は\(0\)以下になる。
また \(x^2-(t^2-t)=-x\) より
\(x^2+x-t(t-1)=0\)
\((x+t)\{x-(t-1)\}=0\)
よって放物線と直線の交点の\(x\)座標は
\(x=-t,t-1\)
(ア) \(0≦t-1≦1\) つまり \(1≦t≦2\) のとき
交点の1つが \(0≦x≦1\) の範囲にあるので図は次の通り。
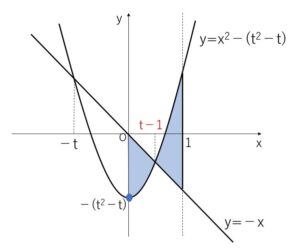
面積\(S\)は
\(S=\displaystyle\int_{0}^{t-1}\{-x-(x^2-t^2+t)\}dx+\displaystyle\int_{t-1}^{1}\{(x^2-t^2+t)-(-x)\}dx\)
(被積分関数を同じにするため、後半の積分区間を入れ替えて)
\(=\displaystyle\int_{0}^{t-1}(-x^2-x+t^2-t)dx+\displaystyle\int_{1}^{t-1}(-x^2-x+t^2-t)dx\)
\(=\left[-\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{2}x^2+(t^2-t)x\right]_{0}^{t-1}+\left[-\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{2}x^2+(t^2-t)x\right]_{1}^{t-1}\)
\(=2×\{-\displaystyle\frac{1}{3}(t-1)^3-\displaystyle\frac{1}{2}(t-1)^2+(t^2-t)(t-1)\}-\left(-\displaystyle\frac{1}{3}-\displaystyle\frac{1}{2}+t^2-t\right)\)
(展開して計算すると)
\(=\displaystyle\frac{4}{3}t^3-4t^2+3t+\displaystyle\frac{1}{2}\)
(イ)\(t-1≧1\) つまり \(t≧2\) のとき
交点は\(0≦x≦1\) の範囲にないので図は次の通り。
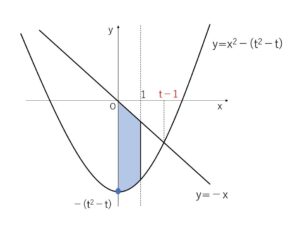
面積\(S\)は
\(S=\displaystyle\int_{0}^{1}\{-x-(x^2-t^2+t)\}dx\)
\(=\displaystyle\int_{0}^{1}(-x^2-x+t^2-t)dx\)
\(=\left[-\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{2}x^2+(t^2-t)x\right]_{0}^{1}\)
\(=-\displaystyle\frac{1}{3}-\displaystyle\frac{1}{2}+(t^2-t)\)
\(=t^2-t-\displaystyle\frac{5}{6}\)
以上から面積\(S\)は
\(S=\displaystyle\frac{4}{3}t^3-4t^2+3t+\displaystyle\frac{1}{2}\) (\(1≦t≦2\))
\(S=t^2-t-\displaystyle\frac{5}{6}\) (\(t≧2\))
(2)
(1)で求めた\(S\)について、\(t\)で微分すると
\(1≦t≦2\) のとき
\(S’=4t^2-8t+3=(2t-1)(2t-3)\)
\(t≧2\) のとき
\(S’=2t-1\)
よって増減表は次の通り。
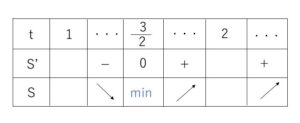
したがって 最小値は \(t=\displaystyle\frac{3}{2}\) のとき
\(S=\displaystyle\frac{4}{3}(\displaystyle\frac{3}{2})^3-4(\displaystyle\frac{3}{2})^2+3(\displaystyle\frac{3}{2})+\displaystyle\frac{1}{2}\)
\(=\displaystyle\frac{1}{2}\)
(例題2)
\(xy\)平面上において、\((0,0)\), \((1,0)\), \((1,1)\) \((0,1)\) を4頂点とする正方形の内部および周を領域\(D\)とする。また、2つの放物線
\(C_1:y=px^2\)
\(C_2:y=-q(x-1)^2+1\)
は共有点をただ1つ持ち、その点で接線を共有している。ただし、\(p,q\)は正の数である。
(1)\(\displaystyle\frac{1}{p}+\displaystyle\frac{1}{q}\) の値を求めよ。
(2)\(D\)のうち \(y≧px^2\) の部分の面積を\(S_1\)とし、\(D\)のうち \(y≦-q(x-1)^2+1\) の部分の面積を\(S_2\)とするとき、\(S=S_1+S_2\) を\(p,q\)を用いて表せ。
(3)\(S\)が最大となる\(p,q\)の値と、\(S\)の最大値を求めよ。
(解答)
(1)
\(px^2=-q(x-1)^2+1\) より
\((p+q)x^2-2qx+q-1=\)・・・①
①が重解をもつとき\(C_1,C_2\)が接するので
\(\displaystyle\frac{D}{4}=0\)
\(q^2-(p+q)(q-1)=0\)
\(-pq+p+q=0\)
\(p,q>0\) より両辺\(pq\)で割って
\(-1+\displaystyle\frac{1}{q}+\displaystyle\frac{1}{p}=0\)
\(\displaystyle\frac{1}{p}+\displaystyle\frac{1}{q}=1\)
(2)
接点の\(x\)座標は①の重解だから
\(x=\displaystyle\frac{q}{p+q}\)
\(p,q>0\)より
\(0<\displaystyle\frac{q}{p+q}<\displaystyle\frac{p+q}{p+q}=1\)
よって、接点の\(x\)座標は \(0<x<1\) の範囲にある。
また、\(C_1\)は\(0\)以上の値、\(C_2\)は\(1\)以下の値をとるので
接点は\(D\)内にある。
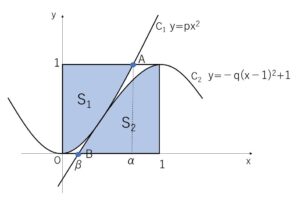
図において
点\(A\)の\(x\)座標\(α\)は
\(px^2=1\) を解いて
\(x=±\displaystyle\frac{1}{\sqrt{p}}\)
大きい方が\(α\)だから
\(α=\displaystyle\frac{1}{\sqrt{p}}\)
点\(B\)の\(x\)座標\(β\)は
\(-q(x-1)^2+1=0\) を解いて
\(x=±\displaystyle\frac{1}{\sqrt{q}}+1\)
このうち小さいほうが\(β\)だから
\(β=-\displaystyle\frac{1}{\sqrt{q}}+1\)
したがって
\(S_1=\displaystyle\int_{0}^{\frac{1}{\sqrt{p}}}(1-px^2)dx\)
\(=\left[x-\displaystyle\frac{1}{3}px^3\right]_{0}^{\frac{1}{\sqrt{p}}}\)
\(=\displaystyle\frac{1}{\sqrt{p}}-\displaystyle\frac{1}{3\sqrt{p}}\)
\(=\displaystyle\frac{2}{3\sqrt{p}}\)
\(S_2=\displaystyle\int_{-\frac{1}{\sqrt{q}}+1}^{1}\{-q(x-1)^2+1\}dx\)
\(=\left[-\displaystyle\frac{q}{3}(x-1)^3+x\right]_{-\frac{1}{\sqrt{q}}+1}^{1}\)
\(=1-\left(\displaystyle\frac{1}{3\sqrt{q}}-\displaystyle\frac{1}{\sqrt{q}}+1\right)\)
\(=\displaystyle\frac{2}{3\sqrt{q}}\)
以上より
\(S=\displaystyle\frac{2}{3}(\displaystyle\frac{1}{\sqrt{p}}+\displaystyle\frac{1}{\sqrt{q}})\)
(3)
\(\displaystyle\frac{1}{\sqrt{p}}+\displaystyle\frac{1}{\sqrt{q}}\) の最大値を求めます。つまり条件付き最大(最小)問題です。
したがって別の方法を模索すると、\(\displaystyle\frac{1}{p}+\displaystyle\frac{1}{q}=1\)を活かすために、\(\displaystyle\frac{1}{\sqrt{p}}+\displaystyle\frac{1}{\sqrt{q}}\) のほうを2乗することを考えます。(正の数なので2乗して最大値を考えてもよい)
他にもいろいろ解法があると思いますが、別解については少しだけ最後に話したいと思います。
\(S=\displaystyle\frac{2}{3}(\displaystyle\frac{1}{\sqrt{p}}+\displaystyle\frac{1}{\sqrt{q}})\) より
\(F=\displaystyle\frac{1}{\sqrt{p}}+\displaystyle\frac{1}{\sqrt{q}}\) の最大値を考えればよい。
\(F>0\) より \(F^2\) の最大値を求めればよく
\(p,q>0\), \(\displaystyle\frac{1}{p}+\displaystyle\frac{1}{q}=1\) に注意して
\(F^2=\displaystyle\frac{2}{\sqrt{pq}}+\displaystyle\frac{1}{p}+\displaystyle\frac{1}{q}\)
\(=2\sqrt{\displaystyle\frac{1}{p}\cdot\displaystyle\frac{1}{q}}+1\)
\(=2\sqrt{\displaystyle\frac{1}{p}(1-\displaystyle\frac{1}{p})}+1\)
\(=2\sqrt{-(\displaystyle\frac{1}{p}-\displaystyle\frac{1}{2})^2+\displaystyle\frac{1}{4}}+1\)・・・②
ここで、
\(\displaystyle\frac{1}{q}=1-\displaystyle\frac{1}{p}\) と \(q>0\) より
\(1-\displaystyle\frac{1}{p}>0\)
\(\displaystyle\frac{1}{p}<1\)
\(p>0\) とあわせて
\(0<\displaystyle\frac{1}{p}<1\)
この範囲における②の最大値は
\(\displaystyle\frac{1}{p}=\displaystyle\frac{1}{2}\) のとき
つまり \(p=2\) で
\(F^2=2\sqrt{\displaystyle\frac{1}{4}}+1=2\)
\(F\)の最大値は \(\sqrt{2}\) となるから
\(S\)の最大値は
\(S=\displaystyle\frac{2\sqrt{2}}{3}\)
このとき
\(\displaystyle\frac{1}{q}=1-\displaystyle\frac{1}{2}=\displaystyle\frac{1}{2}\)
よって \(q=2\)
※別解について
他にも、条件式 \(\displaystyle\frac{1}{p}+\displaystyle\frac{1}{q}=1\) を
\((\displaystyle\frac{1}{\sqrt{p}})^2+(\displaystyle\frac{1}{\sqrt{q}})^2=1\)
と見れば、円上の点に置き換えることができて
\(\displaystyle\frac{1}{\sqrt{p}}=\cosθ\), \(\displaystyle\frac{1}{\sqrt{q}}=\sinθ\)
(\(\displaystyle\frac{1}{\sqrt{p}},\displaystyle\frac{1}{\sqrt{q}}\) のどちらも正だから、\(0°<θ<90°\))
として、\(S=\displaystyle\frac{2}{3}(\cosθ+\sinθ)\) の最大値を求める方法もあります(三角関数の合成を使う)。
他にはコーシー・シュワルツの不等式を利用しても解けます(私はこれが最初に思いつきました)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→区間で関数の式が違う積分 back→接線と面積③(面積・面積比まとめ)