引き続きグラフの対称性を背景とする定積分の置換積分の例題です。
(例題1)
\(x\)は実数とする。
(1)\(\displaystyle\frac{1}{2^x+1}+\displaystyle\frac{1}{2^{-x}+1}\) を計算せよ。
(2)\(\displaystyle\int_{-\frac{π}{2}}^{\frac{π}{2}}\displaystyle\frac{\cos^2x}{2^x+1}dx\) を求めよ。
(解答)
(1)
\(\displaystyle\frac{1}{2^x+1}+\displaystyle\frac{1}{2^{-x}+1}\)
\(=\displaystyle\frac{1}{2^x+1}+\displaystyle\frac{2^x}{1+2^x}\)
\(=\displaystyle\frac{1+2^x}{2^x+1}\)
\(=1\)
(2)
\(I=\displaystyle\int_{-\frac{π}{2}}^{\frac{π}{2}}\displaystyle\frac{\cos^2x}{2^x+1}dx\)
\(x=-t\) で置換すると
\(I=\displaystyle\int_{\frac{π}{2}}^{-\frac{π}{2}}\displaystyle\frac{\cos^2(-t)}{2^{-t}+1}(-dt)\)
よって
\(I=\displaystyle\int_{-\frac{π}{2}}^{\frac{π}{2}}\displaystyle\frac{\cos^2t}{2^{-t}+1}dt\)
ゆえに
\(I+I=\displaystyle\int_{-\frac{π}{2}}^{\frac{π}{2}}(\displaystyle\frac{\cos^2x}{2^x+1}+\displaystyle\frac{\cos^2x}{2^{-x}+1})dx\)
(1)の結果から
\(2I=\displaystyle\int_{-\frac{π}{2}}^{\frac{π}{2}}\cos^2xdx\)
\(\cos^2x\) は偶関数だから
\(I=\displaystyle\frac{1}{2}\cdot2\displaystyle\int_{0}^{\frac{π}{2}}\cos^2xdx\)
\(=\displaystyle\int_{0}^{\frac{π}{2}}\displaystyle\frac{1+\cos2x}{2}dx\)
\(=\left[\displaystyle\frac{1}{2}x+\displaystyle\frac{\sin2x}{4}\right]_{0}^{\frac{π}{2}}\)
\(=\displaystyle\frac{π}{4}\)
(例題2)
(1)連続関数\(f(x)\)が、すべての実数\(x\)について \(f(π-x)=f(x)\) をみたすとき、\(\displaystyle\int_{0}^{π}\left(x-\displaystyle\frac{π}{2}\right)f(x)dx=0\) がなりたつことを証明せよ。
(2)\(\displaystyle\int_{0}^{π}\displaystyle\frac{x\sin^3x}{4-\cos^2x}dx\) を求めよ。
(解答)
(1)
\(I=\displaystyle\int_{0}^{π}\left(x-\displaystyle\frac{π}{2}\right)f(x)dx\) とおく。
\(x=π-t\) で置換すると
\(I=\displaystyle\int_{π}^{0}\left(π-t-\displaystyle\frac{π}{2}\right)f(π-t)(-dt)\)
(\(f(π-x)=f(x)\) より)
\(=\displaystyle\int_{0}^{π}\left(\displaystyle\frac{π}{2}-t\right)f(t)dt\)
\(=-\displaystyle\int_{0}^{π}\left(t-\displaystyle\frac{π}{2}\right)f(t)dt\)
したがって
\(I=-I\) となるから \(2I=0\)
\(I=0\)
(2)
\(J=\displaystyle\int_{0}^{π}\displaystyle\frac{x\sin^3x}{4-\cos^2x}dx\) とおく。
\(f(x)=\displaystyle\frac{\sin^3x}{4-\cos^2x}\) とおくと
\(f(π-x)=\displaystyle\frac{\sin^3(π-x)}{4-\cos^2(π-x)}\)
\(=\displaystyle\frac{\sin^3x}{4-(-\cos x)^2}\)
\(=\displaystyle\frac{\sin^3x}{4-\cos^2x}\)
\(=f(x)\)
となるから、\(f(π-x)=f(x)\) を満たす。
したがって(1)より
\(\displaystyle\int_{0}^{π}xf(x)dx=\displaystyle\int_{0}^{π}\displaystyle\frac{π}{2}f(x)dx\)
が成り立つので
\(J=\displaystyle\int_{0}^{π}\displaystyle\frac{x\sin^3x}{4-\cos^2x}dx=\displaystyle\frac{π}{2}\displaystyle\int_{0}^{π}\displaystyle\frac{\sin^3x}{4-\cos^2x}dx\)・・・①
①の右辺を計算すると
\(J=\displaystyle\frac{π}{2}\displaystyle\int_{0}^{π}\displaystyle\frac{\sin^3x}{4-\cos^2x}dx\)
(\(\sin^2x=1-\cos^2x\) を用いると、導関数接触型になる)
\(=\displaystyle\frac{π}{2}\displaystyle\int_{0}^{π}\displaystyle\frac{1-\cos^2x}{4-\cos^2x}\cdot\sin xdx\)
(\(\cos x=t\) と置換すると)
\(=\displaystyle\frac{π}{2}\displaystyle\int_{1}^{-1}\displaystyle\frac{1-t^2}{4-t^2}(-dt)\)
(上端下端入れ替え)
\(=\displaystyle\frac{π}{2}\displaystyle\int_{-1}^{1}\displaystyle\frac{1-t^2}{4-t^2}dt\)
(偶関数の定積分より)
\(=π\displaystyle\int_{0}^{1}\displaystyle\frac{1-t^2}{4-t^2}dt\)
(分子の次数を下げる)
\(=π\displaystyle\int_{0}^{1}\displaystyle\frac{(4-t^2)-3}{4-t^2}dt\)
\(=π\displaystyle\int_{0}^{1}\left\{1-\displaystyle\frac{3}{(2-t)(2+t)}\right\}dt\)
(部分分数分解して)
\(=π\displaystyle\int_{0}^{1}\left\{1-\displaystyle\frac{3}{4}\left(\displaystyle\frac{1}{2-t}+\displaystyle\frac{1}{2+t}\right)\right\}dt\)
\(=π\left[x-\displaystyle\frac{3}{4}\left(-\log|2-t|+\log|2+t|\right)\right]_{0}^{1}\)
\(=π(1-\displaystyle\frac{3}{4}\log3)\)
したがって
\(J=π(1-\displaystyle\frac{3}{4}\log3)\)
(参考)
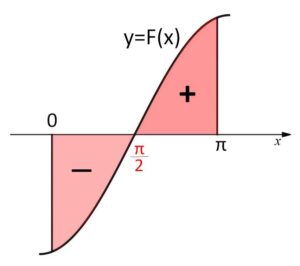
\(f(π-x)=f(x)\) より \(f(x)\) は \(x=\displaystyle\frac{π}{2}\) について対称(線対称)。
\(y=x-\displaystyle\frac{π}{2}\) は、点\((\displaystyle\frac{π}{2},0)\) について対称(点対称)であることから、
\(F(x)=\left(x-\displaystyle\frac{π}{2}\right)f(x)\) が点\((\displaystyle\frac{π}{2},0)\) について対称
です。このことからも面積を考えれば
\(\displaystyle\int_{0}^{π}\left(x-\displaystyle\frac{π}{2}\right)f(x)dx=0\)
が成り立つことが分かります。実際、数式で点対称であることを確認すると
\(F(\displaystyle\frac{π}{2}-t)=-t\cdot f(\displaystyle\frac{π}{2}-t)\)
\(F(\displaystyle\frac{π}{2}+t)=t\cdot f(\displaystyle\frac{π}{2}+t)\)
また \(f(π-x)=f(x)\) より、\(x=\displaystyle\frac{π}{2}+t\) を代入すると
\(f(\displaystyle\frac{π}{2}-t)=f(\displaystyle\frac{π}{2}+t)\) となるから
\(-F(\displaystyle\frac{π}{2}-t)=F(\displaystyle\frac{π}{2}+t)\)・・・(※) (点\((\displaystyle\frac{π}{2},0)\) について対称)
です。
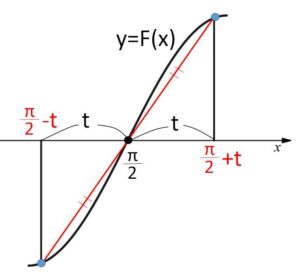
なお(※)で \(\displaystyle\frac{π}{2}+t=x\) と置き換えると
\(-F(π-x)=F(x)\)
となります。これも点\((\displaystyle\frac{π}{2},0)\) について対称であることを示す等式になります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角関数の置換積分と区間分割 back→対称性と定積分①(King Property)