積分区間が幅\(π\)である、三角関数の置換積分の例題です。
(例題1)
\(I=\displaystyle\int_{0}^{nπ}e^{-x}|\sin x|dx\) (\(n\)は自然数) を求めよ。
絶対値が無い \(y=e^{-x}\sin x\) のグラフは微分すると正確に分かりますが、\(y=±e^{-x}\) を境界として振動するグラフになります(極値は \(y=±e^{-x}\) 上には無いが)。したがって \(y=f(x)\) のグラフは、\(y=e^{-x}\sin x\) のグラフの負の部分を折り返せばよいので、大きさが徐々に小さくなる山(横幅は\(π\))が連なった形状をしています(減衰曲線と呼ばれる)。この山の面積の総和が求める定積分の値です。
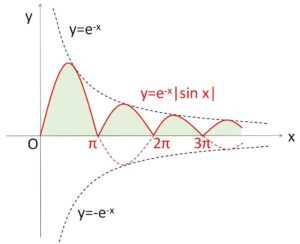
(解答)
まず、\(|\sin x|\) を外すために、積分区間を\(π\)ずつ分割します。
\(I=\displaystyle\int_{0}^{nπ}e^{-x}|\sin x|dx\)
\(=\displaystyle\int_{0}^{π}e^{-x}|\sin x|dx+\displaystyle\int_{π}^{2π}e^{-x}|\sin x|dx+\cdots+\displaystyle\int_{(n-1)π}^{nπ}e^{-x}|\sin x|dx\)
\(=\displaystyle\sum_{k=1}^{n}\displaystyle\int_{(k-1)π}^{kπ}e^{-x}|\sin x|dx\)
ここで、\(t=x-(k-1)π\) (\(x=t+(k-1)π\)) と置換すると
\(I=\displaystyle\sum_{k=1}^{n}\displaystyle\int_{0}^{π}e^{-t-(k-1)π}|\sin \{t+(k-1)π\}|dt\)
(\(e^{-(k-1)π}\) は積分変数に無関係。また、\(\sin \{t+(k-1)π\}=(-1)^{k-1}\sin t\))
\(=\displaystyle\sum_{k=1}^{n}e^{-(k-1)π}\displaystyle\int_{0}^{π}e^{-t}|(-1)^{k-1}\sin t|dt\)
\(=\displaystyle\sum_{k=1}^{n}e^{-(k-1)π}\displaystyle\int_{0}^{π}e^{-t}|\sin t|dt\)
(\(0≦t≦π\) のとき、\(\sin t≧0\))
\(=\displaystyle\sum_{k=1}^{n}e^{-(k-1)π}\displaystyle\int_{0}^{π}e^{-t}\sin tdt\)
定積分は、(i)部分積分を2回用いて同形出現させるか、(ii)\(e^{-t}\sin t,e^{-t}\cos t\) をセットにしてそれぞれ微分して、連立方程式の要領で求める ことになります。今回は後者でやろうと思います。
定積分について
\((e^{-t}\sin t)’=-e^{-t}\sin t+e^{-t}\cos t\)・・・①
\((e^{-t}\cos t)’=-e^{-t}\sin t-e^{-t}\cos t\)・・・②
だから、①+② をして\(0\)から\(π\)まで積分すると
\(-2\displaystyle\int_{0}^{π}e^{-t}\sin tdt=[e^{-t}\sin t+e^{-t}\cos t]_{0}^{π}\)
よって
\(\displaystyle\int_{0}^{π}e^{-t}\sin tdt=\displaystyle\frac{e^{-π}+1}{2}\) (定数値)
したがって
\(I=\displaystyle\frac{e^{-π}+1}{2}\displaystyle\sum_{k=1}^{n}e^{-(k-1)π}\)
(公比が\(e^{-π}\) の等比数列の和)
\(=\displaystyle\frac{e^{-π}+1}{2}\cdot\displaystyle\frac{e^{0}\{1-(e^{-π})^n\}}{1-e^{-π}}\)
(分母分子\(e^{π}\)倍して)
\(=\displaystyle\frac{(e^{π}+1)\{1-(e^{-π})^n\}}{2(e^{π}-1)}\)
(例題2)
\(n\)は正の整数とする。
(1)\(\displaystyle\int_{0}^{π}e^{\frac{t}{n}}\sin tdt\) を求めよ。
(2)\(J=\displaystyle\int_{0}^{π}e^{x}|\sin nx|dx\) を求めよ。
(1)
なお(1)は(2)の計算途中で出てくる定積分になっています。
\((e^{\frac{t}{n}}\sin t)’=\displaystyle\frac{1}{n}e^{\frac{t}{n}}\sin t+e^{\frac{t}{n}}\cos t\)・・・①
\((e^{\frac{t}{n}}\cos t)’=-e^{\frac{t}{n}}\sin t+\displaystyle\frac{1}{n}e^{\frac{t}{n}}\cos t\)・・・②
①-n×② をして、\(0\)から\(π\)まで積分すると
\((\displaystyle\frac{1}{n}+n)\displaystyle\int_{0}^{π}e^{\frac{t}{n}}\sin tdt=[e^{\frac{t}{n}}\sin t-ne^{\frac{t}{n}}\cos t]_{0}^{π}\)
\(\displaystyle\frac{n^2+1}{n}\displaystyle\int_{0}^{π}e^{\frac{t}{n}}\sin tdt=ne^{\frac{π}{n}}+n\)
したがって
\(\displaystyle\int_{0}^{π}e^{\frac{t}{n}}\sin tdt=\displaystyle\frac{n^2(1+e^{\frac{π}{n}})}{n^2+1}\)
(2)
\(J=\displaystyle\int_{0}^{π}e^{x}|\sin nx|dx\)
\(nx=u\) で置換すると \(ndx=du\) だから
\(J=\displaystyle\int_{0}^{nπ}e^{\frac{u}{n}}|\sin u|\displaystyle\frac{1}{n}du\)
(この後は例題1とほとんど同じです。区間分割して)
\(=\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{π}\displaystyle\int_{(k-1)π}^{kπ}e^{\frac{u}{n}}|\sin u|du\)
(\(t=u-(k-1)π\) で置換して)
\(=\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{π}\displaystyle\int_{0}^{π}e^{\frac{t+(k-1)π}{n}}|\sin \{t+(k-1)π\}|dt\)
(\(e^{\frac{(k-1)π}{n}}\) は積分変数に無関係)
\(=\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{π}e^{\frac{(k-1)π}{n}}\displaystyle\int_{0}^{π}e^{\frac{t}{n}}|(-1)^{k-1}\sin t|dt\)
\(=\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{π}(e^{\frac{π}{n}})^{k-1}\displaystyle\int_{0}^{π}e^{\frac{t}{n}}\sin tdt\)
((1)より定積分の部分は定数値だから)
\(=\displaystyle\frac{1}{n}\cdot\displaystyle\frac{n^2(1+e^{\frac{π}{n}})}{n^2+1}\displaystyle\sum_{k=1}^{π}(e^{\frac{π}{n}})^{k-1}\)
(公比\(e^{\frac{π}{n}}\)の等比数列の和を計算して)
\(=\displaystyle\frac{n(1+e^{\frac{π}{n}})}{n^2+1}\cdot\displaystyle\frac{1\cdot\{1-(e^{\frac{π}{n}})^n\}}{1-e^{\frac{π}{n}}}\)
\(=\displaystyle\frac{n}{n^2+1}\cdot\displaystyle\frac{(1-e^π)(1+e^{\frac{π}{n}})}{1-e^{\frac{π}{n}}}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→定積分と微分 back→対称性と定積分②