絶対値を含む関数の定積分の最大最小問題です。
解法の基本は場合分けして絶対値を外すことです。
(例題1)
\(a>0\)、\(t>0\) に対して定積分
\(S(a,t)=\displaystyle\int_{0}^{a}\left|e^{-x}-\displaystyle\frac{1}{t}\right|dx\)
を考える。\(a\)を固定したとき、\(t\)の関数\(S(a,t)\)の最小値\(m(a)\)を求めよ。
また、積分区間は\(0\)から\(a\)なので、\(y=e^{-x}\) の端点は \(e^{-0}=1\)、\(e^{-a}\) になるから、\(y=e^{-x}\) と \(y=\displaystyle\frac{1}{t}\) の位置関係(交わるかどうか)を考えると
①\(\displaystyle\frac{1}{t}>1\)
②\(e^{-a}≦\displaystyle\frac{1}{t}≦1\)
③\(0<\displaystyle\frac{1}{t}<e^{-a}\)
の3パターンに場合分けすることになります。積分計算すると\(t\)の関数になるので(\(a\)は文字定数として残る)、\(t\)を変化させたときの最小値を求めることになります。解答では素直にこの3パターンについて検討することにしますが、①③は図で\(t\)を変化させたときの面積の増減を考えると、①③で最小値をとることは無いことがすぐに分かります(参考参照)。
なお\(a\)の固定については場合分けの必要はないです。(どこで固定しても同じ)
(解答)

\(y=e^{-x}\) と \(y=\displaystyle\frac{1}{t}\) のグラフの上下関係を考えると
①\(0<t<1\) のとき
\(S(a,t)=\displaystyle\int_{0}^{a}\left|e^{-x}-\displaystyle\frac{1}{t}\right|dx\)
\(=\displaystyle\int_{0}^{a}\left(\displaystyle\frac{1}{t}-e^{-x}\right)dx\)
\(=\left[\displaystyle\frac{1}{t}x+e^{-x}\right]_{0}^{a}\)
\(=\displaystyle\frac{1}{t}a+e^{-a}-1\) (\(a>0\)より単調減少)
②\(1≦t≦e^{a}\) のとき
\(e^{-x}=\displaystyle\frac{1}{t}\) を\(x\)について解くと \(x=\log t\) だから
\(S(a,t)=\displaystyle\int_{0}^{a}\left|e^{-x}-\displaystyle\frac{1}{t}\right|dx\)
\(=\displaystyle\int_{0}^{\log t}\left(e^{-x}-\displaystyle\frac{1}{t}\right)dx+\displaystyle\int_{\log t}^{a}\left(\displaystyle\frac{1}{t}-e^{-x}\right)dx\)
\(=\left[-e^{-x}-\displaystyle\frac{1}{t}x\right]_{0}^{\log t}+\left[\displaystyle\frac{1}{t}x+e^{-x}\right]_{\log t}^{a}\)
\(=\left(-\displaystyle\frac{1}{t}-\displaystyle\frac{\log t}{t}+1\right)+\left(\displaystyle\frac{a}{t}+e^{-a}-\displaystyle\frac{\log t}{t}-\displaystyle\frac{1}{t}\right)\)
\(=-\displaystyle\frac{2}{t}-\displaystyle\frac{2\log t}{t}+\displaystyle\frac{a}{t}+e^{-a}+1\)
③\(t>e^{a}\) のとき
\(S(a,t)=\displaystyle\int_{0}^{a}\left|e^{-x}-\displaystyle\frac{1}{t}\right|dx\)
\(=\displaystyle\int_{0}^{a}\left(e^{-x}-\displaystyle\frac{1}{t}\right)dx\)
(①で符号を反対にするだけなので)
\(=-\displaystyle\frac{1}{t}a-e^{-a}+1\) (\(a>0\)より単調増加)
よって最小値は②のときにとり
\(S(a,t)=f(t)=-\displaystyle\frac{2}{t}-\displaystyle\frac{2\log t}{t}+\displaystyle\frac{a}{t}+e^{-a}+1\)
(\(1≦t≦e^{a}\)) について
\(f'(t)=\displaystyle\frac{2}{t^2}-2\cdot\displaystyle\frac{1-\log t}{t^2}-\displaystyle\frac{a}{t^2}\)
\(=\displaystyle\frac{2\log t-a}{t^2}=\displaystyle\frac{\log t^2-\log e^{a}}{t^2}\)
\(t^2=e^{a}\) を解くと \(t=e^{\frac{a}{2}}\) だから
\(1<t<e^{\frac{a}{2}}\) のとき \(f'(t)<0\)
\(e^{\frac{a}{2}}<t<e^{a}\) のとき \(f'(t)>0\)
したがって\(S(a,t)\)は \(t=e^{\frac{a}{2}}\) のとき最小値
\(m(a)=-2e^{-\frac{a}{2}}-2\cdot\displaystyle\frac{a}{2}e^{-\frac{a}{2}}+a\cdot e^{-\frac{a}{2}}+e^{-a}+1\)
\(=e^{-a}-2e^{-\frac{a}{2}}+1\)
をとる。
(参考)
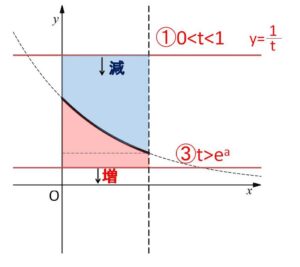
\(y=\displaystyle\frac{1}{t}\) のグラフを上から下げていくと (\(t\)を大きくしていくと)
①では囲まれた図形の面積が減少、③では面積が増加するので、\(S(a,t)\)はそれぞれ単調減少、単調増加になります。このことを記載して、①③の積分計算を省いても構いません。
(例題2)
実数\(a\)に対し、積分
\(f(a)=\displaystyle\int_{0}^{\frac{π}{4}}|\sin x-a\cos x|dx\)
を考える。\(f(a)\)の最小値を求めよ。
また、\(\sin x\) と \(a\cos x\) の上下関係を考えるよりも、\(\cos x\) でくくることにより、\(\tan x\) と \(a\) の上下関係を考えるほうが分かりやすいです(定数分離)。
(解答)
\(f(a)=\displaystyle\int_{0}^{\frac{π}{4}}|\sin x-a\cos x|dx\)
\(=\displaystyle\int_{0}^{\frac{π}{4}}|\cos x(\tan x-a)|dx\)
\(=\displaystyle\int_{0}^{\frac{π}{4}}\cos x|\tan x-a|dx\)
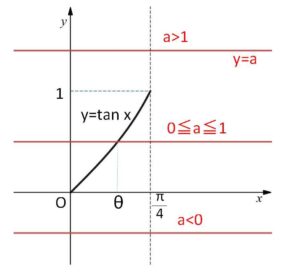
\(y=\tan x\) と \(y=a\) で囲まれる面積を考えると、\(f(a)\)は
\(a≦0\) のとき 単調減少、\(a≧1\) のとき単調増加になるので、\(0≦a≦1\) のとき最小値をとる。
\(0≦a≦1\) のとき、\(y=\tan x\) と \(y=a\) のグラフは交点をただ1つもち、
\(\tanθ=a\)・・・① (\(0≦θ≦\displaystyle\frac{π}{4}\))
を満たす\(θ\)が存在する。
\(0≦x≦θ\) のとき、絶対値の中身が\(0\)以下になるから
\(f(a)=\displaystyle\int_{0}^{θ}(a\cos x-\sin x)dx+\displaystyle\int_{θ}^{\frac{π}{4}}(\sin x-a\cos x)dx\)
\(=[a\sin x+\cos x]_{0}^{θ}+[-\cos x-a\sin x]_{θ}^{\frac{π}{4}}\)
\(=(a\sinθ+\cosθ-1)+(-\displaystyle\frac{1}{\sqrt{2}}-\displaystyle\frac{a}{\sqrt{2}}+\cosθ+a\sinθ)\)
\(=2a\sinθ+2\cosθ-\displaystyle\frac{a}{\sqrt{2}}-1-\displaystyle\frac{1}{\sqrt{2}}\)
①より
\(f(a)=2\tanθ\sinθ+2\cosθ-\displaystyle\frac{\tanθ}{\sqrt{2}}-1-\displaystyle\frac{1}{\sqrt{2}}\)
\(=2\cdot\displaystyle\frac{\sin^2θ+\cos^2θ}{\cosθ}-\displaystyle\frac{\tanθ}{\sqrt{2}}-1-\displaystyle\frac{1}{\sqrt{2}}\)
\(=\displaystyle\frac{2}{\cosθ}-\displaystyle\frac{\sqrt{2}\tanθ}{2}-\displaystyle\frac{2+\sqrt{2}}{2}\)
ここで、\(a\)を \(a:0 \to 1\) と変化させると、\(θ\)は \(θ:0 \to \displaystyle\frac{π}{4}\) と変化するので
\(g(θ)=\displaystyle\frac{2}{\cosθ}-\displaystyle\frac{\sqrt{2}\tanθ}{2}-\displaystyle\frac{2+\sqrt{2}}{2}\) (\(0≦θ≦\displaystyle\frac{π}{4}\))
の最小値を求めればよい。
\(g'(θ)=\displaystyle\frac{2\sinθ}{\cos^2θ}-\displaystyle\frac{\sqrt{2}}{2\cos^2θ}\)\(=\displaystyle\frac{4(\sinθ-\displaystyle\frac{\sqrt{2}}{4})}{2\cos^2θ}\)
\(\sin 0<\displaystyle\frac{\sqrt{2}}{4}<\sin\displaystyle\frac{π}{4}\) より、
\(\sinα=\displaystyle\frac{\sqrt{2}}{4}\)・・・② (\(0<α<\displaystyle\frac{π}{4}\))
を満たす\(α\)がただ1つ存在し、\(θ=α\) のときに\(g(θ)\)は最小値をとる。
②より
\(\cosα=\sqrt{1-\displaystyle\frac{2}{16}}=\displaystyle\frac{\sqrt{14}}{4}\)
\(\tanα=\displaystyle\frac{\sqrt{2}}{\sqrt{14}}=\displaystyle\frac{1}{\sqrt{7}}\ (=a)\)
したがって\(f(a)\)の最小値は
\(g(α)=\displaystyle\frac{2}{\cosα}-\displaystyle\frac{\sqrt{2}\tanα}{2}-\displaystyle\frac{2+\sqrt{2}}{2}\)
\(=\displaystyle\frac{8}{\sqrt{14}}-\displaystyle\frac{\sqrt{2}}{2\sqrt{7}}-\displaystyle\frac{2+\sqrt{2}}{2}\)
\(=\displaystyle\frac{8\sqrt{14}}{14}-\displaystyle\frac{\sqrt{14}}{14}-\displaystyle\frac{2+\sqrt{2}}{2}\)
\(=\displaystyle\frac{\sqrt{14}-2-\sqrt{2}}{2}\) (\(a=\displaystyle\frac{1}{\sqrt{7}}\))
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→積分方程式① back→定積分と最大最小①