微分の定義を利用する、定積分を含む極限の例題です。
(例題)
次の極限を求めよ。
(1)\(\displaystyle\lim_{x \to 1}\displaystyle\frac{1}{x-1}\displaystyle\int_{1}^{x}te^{-t}dt\)
(2)\(\displaystyle\lim_{x \to 0}\displaystyle\frac{1}{x}\displaystyle\int_{0}^{x}e^{t^2}dt\)
(3)\(\displaystyle\lim_{x \to 1}\displaystyle\frac{1}{x-1}\displaystyle\int_{1}^{x^2}\displaystyle\frac{1}{\sqrt{t^2+1}}dt\)
(1)(3)については積分計算が可能ですが、(2)は不可です。よってこの威力が発揮できます。また積分計算可能でも微分の定義を利用すると極限計算が非常に楽になります。
一応(1)で積分計算する場合の解法もやっておきます。また(2)では面積の大小比較ではさみうちの原理を利用する別解もあります。
(解答)
(1)
\(\displaystyle\lim_{x \to 1}\displaystyle\frac{1}{x-1}\displaystyle\int_{1}^{x}te^{-t}dt\)
\(te^{-t}\) の原始関数の1つを\(F(t)\) とすると
\(F'(t)=te^{-t}\)
よって
\(\displaystyle\lim_{x \to 1}\displaystyle\frac{1}{x-1}\displaystyle\int_{1}^{x}te^{-t}dt\)
\(=\displaystyle\lim_{x \to 1}\displaystyle\frac{F(x)-F(1)}{x-1}\)
\(=F'(1)\)
\(=e^{-1}\)
(別解)素直に積分計算すると
\(\displaystyle\int_{1}^{x}te^{-t}dt\)
(部分積分をして)
\(=[t(-e^{-t})]_{1}^{x}+\displaystyle\int_{1}^{x}e^{-t}\)
\(=-xe^{-x}+e^{-1}+[-e^{-t}]_{1}^{x}\)
\(=-xe^{-x}-e^{-x}+2e^{-1}\)
よって
\(\displaystyle\lim_{x \to 1}\displaystyle\frac{1}{x-1}\displaystyle\int_{1}^{x}te^{-t}dt\)
\(=\displaystyle\lim_{x \to 1}\displaystyle\frac{-\displaystyle\frac{x}{e^{x}}-\displaystyle\frac{1}{e^{x}}+\displaystyle\frac{2}{e}}{x-1}\)
\(=\displaystyle\lim_{x \to 1}\displaystyle\frac{-x-1+2e^{x-1}}{x-1}\cdot\displaystyle\frac{1}{e^x}\)
(\(x-1=s\) とおくと)
\(=\displaystyle\lim_{x \to 1,s \to 0}\displaystyle\frac{-s-2+2e^{s}}{s}\cdot\displaystyle\frac{1}{e^x}\)
\(=\displaystyle\lim_{x \to 1,s \to 0}\left(2\cdot\displaystyle\frac{e^{s}-1}{s}-1\right)\cdot\displaystyle\frac{1}{e^x}\)
\(=(2\cdot1-1)\cdot\displaystyle\frac{1}{e^1}\)
\(=\displaystyle\frac{1}{e}\)
(2)
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{1}{x}\displaystyle\int_{0}^{x}e^{t^2}dt\)
\(e^{t^2}\) の原始関数の1つを \(F(t)\) とおくと
\(F'(t)=e^{t^2}\) だから
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{1}{x}\displaystyle\int_{0}^{x}e^{t^2}dt\)
\(=\displaystyle\lim_{x \to 0}\displaystyle\frac{F(x)-F(0)}{x-0}\)
\(=F'(0)\)
\(=1\)
(別解)面積比較
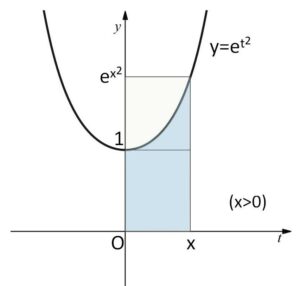
(i)\(x>0\) のとき
図より面積の大小を考えると
\(x\cdot 1<\displaystyle\int_{0}^{x}e^{t^2}dt<xe^{x^2}\)
\(x\)で辺々割って
\(1<\displaystyle\frac{1}{x}\displaystyle\int_{0}^{x}e^{t^2}dt<e^{x^2}\)
はさみうちの原理より
\(\displaystyle\lim_{x \to +0}\displaystyle\frac{1}{x}\displaystyle\int_{0}^{x}e^{t^2}dt=1\)
(ii)\(x<0\) のとき
同様に
\(-x\cdot 1<\displaystyle\int_{x}^{0}e^{t^2}dt<-xe^{x^2}\)
よって
\(-x<-\displaystyle\int_{0}^{x}e^{t^2}dt<-xe^{x^2}\)
\(-x\ (>0)\) で辺々割って
\(1<\displaystyle\frac{1}{x}\displaystyle\int_{0}^{x}e^{t^2}dt<e^{x^2}\)
はさみうちの原理より
\(\displaystyle\lim_{x \to -0}\displaystyle\frac{1}{x}\displaystyle\int_{0}^{x}e^{t^2}dt=1\)
したがって
\(\displaystyle\lim_{x \to 0}\displaystyle\frac{1}{x}\displaystyle\int_{0}^{x}e^{t^2}dt=1\)
(3)
\(\displaystyle\lim_{x \to 1}\displaystyle\frac{1}{x-1}\displaystyle\int_{1}^{x^2}\displaystyle\frac{1}{\sqrt{t^2+1}}dt\)
\(\displaystyle\frac{1}{\sqrt{t^2+1}}\) の原始関数の1つを\(F(t)\)とおくと
\(F'(t)=\displaystyle\frac{1}{\sqrt{t^2+1}}\)
よって
\(\displaystyle\lim_{x \to 1}\displaystyle\frac{1}{x-1}\displaystyle\int_{1}^{x^2}\displaystyle\frac{1}{\sqrt{t^2+1}}dt\)
\(=\displaystyle\lim_{x \to 1}\displaystyle\frac{F(x^2)-F(1)}{x-1}\)
(分母を\(x^2-1\)にするために、\(x+1\) を分母分子に掛ける)
\(=\displaystyle\lim_{x \to 1}\displaystyle\frac{F(x^2)-F(1)}{x^2-1}\cdot(x+1)\)
\(=F'(1)\cdot2\)
\(=\displaystyle\frac{2}{\sqrt{2}}\)
\(=\sqrt{2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→区分求積法① back→積分方程式②