区分求積法による和の極限の計算問題です。
今回は、定積分の幅が\(\displaystyle\int_{0}^{1}\) にならないケースや、対数を利用する場合を扱います。
(例題1)
(1)\(\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{2n}\displaystyle\frac{1}{n+k}\)
(2)\(\displaystyle\lim_{n \to \infty}n\displaystyle\sum_{k=n+1}^{3n}\displaystyle\frac{1}{k^2-2nk-8n^2}\)
(3)\(\displaystyle\lim_{n \to \infty}\left\{\displaystyle\frac{1}{2n+1}+\displaystyle\frac{1}{2n+3}+\displaystyle\frac{1}{2n+5}+\cdots+\displaystyle\frac{1}{2n+(2n-1)}\right\}\)
(解答)
(1)
\(\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{2n}\displaystyle\frac{1}{n+k}=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{2n}\displaystyle\frac{1}{1+\displaystyle\frac{k}{n}}\)
と変形して、\(f(x)=\displaystyle\frac{1}{1+x}\) の積分を考えます。積分区間は、\(k\)に順に代入していくと、\(\displaystyle\frac{1}{n},\displaystyle\frac{2}{n},\cdots,\displaystyle\frac{2n}{n}\) となるので、\(0\)から\(2\) までになります(図と対応させて考えて下さい)。機械的にやるなら、両端の \(\displaystyle\frac{1}{n},\displaystyle\frac{2n}{n}\) で \(n \to \infty\) の極限 (それぞれ、\(0,2\) になる) を考えるとよいでしょう。
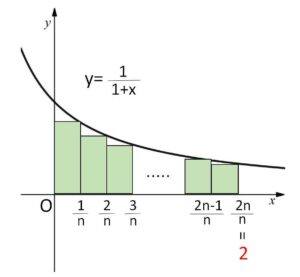
\(\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{2n}\displaystyle\frac{1}{n+k}=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{2n}\displaystyle\frac{1}{1+\displaystyle\frac{k}{n}}\)
\(=\displaystyle\int_{0}^{2}\displaystyle\frac{1}{1+x}dx\)
\(=[\log|1+x|]_{0}^{2}\)
\(=\log3\)
(2)
\(\displaystyle\sum_{k=n+1}^{3n}=\displaystyle\sum_{k=1}^{3n}-\displaystyle\sum_{k=1}^{n}\)
を考えてもよいですし、図から直接積分を考えてもよいです(区間は\(1\)から\(3\)になる)。
\(\displaystyle\lim_{n \to \infty}n\displaystyle\sum_{k=n+1}^{3n}\displaystyle\frac{1}{k^2-2nk-8n^2}\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=n+1}^{3n}\displaystyle\frac{1}{(\displaystyle\frac{k}{n})^2-2(\displaystyle\frac{k}{n})-8}\)
\(=\displaystyle\lim_{n \to \infty}\left\{\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{3n}\displaystyle\frac{1}{(\displaystyle\frac{k}{n})^2-2(\displaystyle\frac{k}{n})-8}-\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{(\displaystyle\frac{k}{n})^2-2(\displaystyle\frac{k}{n})-8}\right\}\)
(どちらも収束して)
\(=\displaystyle\int_{0}^{3}\displaystyle\frac{1}{x^2-2x-8}dx-\displaystyle\int_{0}^{1}\displaystyle\frac{1}{x^2-2x-8}dx\)
\(=\displaystyle\int_{1}^{3}\displaystyle\frac{1}{x^2-2x-8}dx\)
(部分分数分解をする)
\(=\displaystyle\int_{1}^{3}\displaystyle\frac{1}{(x-4)(x+2)}dx\)
\(=\displaystyle\frac{1}{6}\displaystyle\int_{1}^{3}(\displaystyle\frac{1}{x-4}-\displaystyle\frac{1}{x+2})dx\)
\(=\displaystyle\frac{1}{6}[\log|x-4|-\log|x+2|]_{1}^{3}\)
\(=-\displaystyle\frac{1}{6}\log5\)
(別解)
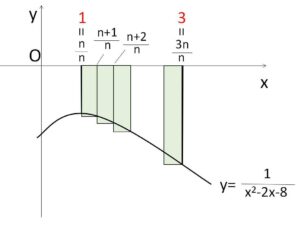
\(\displaystyle\lim_{n \to \infty}n\displaystyle\sum_{k=n+1}^{3n}\displaystyle\frac{1}{k^2-2nk-8n^2}\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=n+1}^{3n}\displaystyle\frac{1}{(\displaystyle\frac{k}{n})^2-2(\displaystyle\frac{k}{n})-8}\)
(上図より)
\(=\displaystyle\int_{1}^{3}\displaystyle\frac{1}{x^2-2x-8}dx\)
(以下同様)
(※)他にも \(k=1\) スタートにする方法もあります
\(\displaystyle\lim_{n \to \infty}n\displaystyle\sum_{k=n+1}^{3n}\displaystyle\frac{1}{k^2-2nk-8n^2}\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=n+1}^{3n}\displaystyle\frac{1}{(\displaystyle\frac{k}{n})^2-2(\displaystyle\frac{k}{n})-8}\)
\(=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{2n}\displaystyle\frac{1}{(1+\displaystyle\frac{k}{n})^2-2(1+\displaystyle\frac{k}{n})-8}\)
\(=\displaystyle\int_{0}^{2}\displaystyle\frac{1}{(1+x)^2-2(1+x)-8}\ dx\)
\(=\displaystyle\int_{0}^{2}\displaystyle\frac{1}{x^2-9}\ dx\)
\(=\displaystyle\int_{0}^{2}\displaystyle\frac{1}{(x-3)(x+3)}\ dx\)
(以下省略。この方法は実質上図のグラフを\(x\)軸方向に\(-1\)平行移動しているだけです)
(3)
\(\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{2n+(2k-1)}=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{2+2\cdot\displaystyle\frac{k}{n}-\displaystyle\frac{1}{n}}\)
となり、\(-\displaystyle\frac{1}{n}\) が邪魔で積分に変換できません。これは \(2k-1\) が飛び飛びになっているのが原因なので、間を埋めるようにするとうまくいきます。もしくは、邪魔な \(-\displaystyle\frac{1}{n}\) の部分をいじって不等式ではさみこむ方法もあります。
\(S_n=\left\{\displaystyle\frac{1}{2n+1}+\displaystyle\frac{1}{2n+3}+\displaystyle\frac{1}{2n+5}+\cdots+\displaystyle\frac{1}{2n+(2n-1)}\right\}\) とおく。
\(S_n=\left\{\displaystyle\frac{1}{2n+1}+\displaystyle\frac{1}{2n+2}+\displaystyle\frac{1}{2n+3}+\cdots+\displaystyle\frac{1}{2n+(2n-1)}+\displaystyle\frac{1}{2n+2n}\right\}\)
\(-\left\{\displaystyle\frac{1}{2n+2}+\displaystyle\frac{1}{2n+4}+\displaystyle\frac{1}{2n+6}+\cdots+\displaystyle\frac{1}{2n+(2n-2)}+\displaystyle\frac{1}{2n+2n}\right\}\)
\(=\displaystyle\sum_{k=1}^{2n}\displaystyle\frac{1}{2n+k}-\displaystyle\frac{1}{2}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{n+k}\)
よって与式は
\(\displaystyle\lim_{n \to \infty}S_n\)
\(=\displaystyle\lim_{n \to \infty}\left(\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{2n}\displaystyle\frac{1}{2+\displaystyle\frac{k}{n}}-\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{1+\displaystyle\frac{k}{n}}\right)\)
\(=\displaystyle\int_{0}^{2}\displaystyle\frac{1}{2+x}dx-\displaystyle\frac{1}{2}\displaystyle\int_{0}^{1}\displaystyle\frac{1}{1+x}dx\)
\(=[\log|2+x|]_{0}^{2}-\displaystyle\frac{1}{2}[\log|1+x|]_{0}^{1}\)
\(=\log4-\log2-\displaystyle\frac{1}{2}\log2\)
\(=\displaystyle\frac{1}{2}\log2\)
(別解)
(分母が正の場合、分母の数が大きいほうが全体としては小さい)
\(\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{2n+2k}<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{2n+(2k-1)}<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{2n+(2k-2)}\) より
\(\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{1+\displaystyle\frac{k}{n}}<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{2n+(2k-1)}<\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{1+\displaystyle\frac{k-1}{n}}\)
\(\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{1+\displaystyle\frac{k}{n}}<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{2n+(2k-1)}<\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{n}\displaystyle\sum_{l=0}^{n-1}\displaystyle\frac{1}{1+\displaystyle\frac{l}{n}}\)
\(n \to \infty\) のとき左辺と右辺は
\(\displaystyle\frac{1}{2}\displaystyle\int_{0}^{1}\displaystyle\frac{1}{1+x}dx=\displaystyle\frac{1}{2}[\log|1+x|]_{0}^{1}=\displaystyle\frac{1}{2}\log2\)
に収束。
よって
(与式)\(=\displaystyle\lim_{n \to \infty}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{2n+(2k-1)}\)\(=\displaystyle\frac{1}{2}\log2\)
(例題2)
次の極限を求めよ。
(1)\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{\sqrt[n]{n(n+1)(n+2)\cdots(2n-1)}}{n}\)
(2)\(\displaystyle\lim_{n \to \infty}\displaystyle\frac{\sqrt[n]{{}_{4n}\mathrm{P}_{2n}}}{n^2}\)
何故かというと、指数を解消でき、積を和の形にできるからです。
(解答)
(1)
\(a_n=\displaystyle\frac{\sqrt[n]{n(n+1)(n+2)\cdots(2n-1)}}{n}\) とおくと
(まず \(\displaystyle\frac{1}{n}\)を累乗根に突っ込んで、\(\displaystyle\frac{k}{n}\) の形をつくります)
\(a_n=\sqrt[n]{\displaystyle\frac{{n(n+1)(n+2)\cdots\{n+(n-1)\}}}{n^n}}\)
(\(n\)で1つずつ割って)
\(=\sqrt[n]{(1+\displaystyle\frac{0}{n})(1+\displaystyle\frac{1}{n})(1+\displaystyle\frac{2}{n})\cdots(1+\displaystyle\frac{n-1}{n})}\)
よって
\(\log a_n=\displaystyle\frac{1}{n}\log(1+\displaystyle\frac{0}{n})(1+\displaystyle\frac{1}{n})(1+\displaystyle\frac{2}{n})\cdots(1+\displaystyle\frac{n-1}{n})\)
\(=\displaystyle\frac{1}{n}\{\log(1+\displaystyle\frac{0}{n})+\log(1+\displaystyle\frac{1}{n})+\cdots+\log(1+\displaystyle\frac{n-1}{n})\}\)
\(=\displaystyle\frac{1}{n}\displaystyle\sum_{k=0}^{n-1}\log(1+\displaystyle\frac{k}{n})\)
ゆえに
\(\displaystyle\lim_{n \to \infty}\log a_n=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=0}^{n-1}\log(1+\displaystyle\frac{k}{n})\)
\(=\displaystyle\int_{0}^{1}\log(1+x)dx\)
(部分積分をして)
\(=[(1+x)\log(1+x)]_{0}^{1}-\displaystyle\int_{0}^{1} dx\)
\(=2\log2-[x]_{0}^{1}\)
\(=2\log2-1\)
(最後に対数を外すので、まとめておく)
\(=\log4-\log e\)
\(=\log\displaystyle\frac{4}{e}\)
したがって
\(\displaystyle\lim_{n \to \infty}\log a_n=\log\displaystyle\frac{4}{e}\)
だから
\(\displaystyle\lim_{n \to \infty}a_n=\displaystyle\frac{4}{e}\)
(2)
\(b_n=\displaystyle\frac{\sqrt[n]{{}_{4n}\mathrm{P}_{2n}}}{n^2}\) とおく。
\(b_n=\sqrt[n]{\displaystyle\frac{\displaystyle\frac{(4n)!}{(4n-2n)!}}{n^{2n}}}=\sqrt[n]{\displaystyle\frac{\displaystyle\frac{(4n)!}{(2n)!}}{n^{2n}}}\)
\(=\sqrt[n]{\displaystyle\frac{4n(4n-1)(4n-2)\cdots(2n+1)}{n^{2n}}}\)
(\(2n+1\) スタートになっているので、\(2n\)に合わせると)
\(=\sqrt[n]{\displaystyle\frac{(2n+2n)(2n+2n-1)(2n+2n-2)\cdots(2n+1)}{n^{2n}}}\)
(積は\(2n\)個あるので、それぞれ\(n\)で割って)
\(=\sqrt[n]{(2+\displaystyle\frac{2n}{n})(2+\displaystyle\frac{2n-1}{n})(2+\displaystyle\frac{2n-2}{n})\cdots(2+\displaystyle\frac{1}{n})}\)
よって
\(\log b_n=\displaystyle\frac{1}{n}\log(2+\displaystyle\frac{2n}{n})(2+\displaystyle\frac{2n-1}{n})(2+\displaystyle\frac{2n-2}{n})\cdots(2+\displaystyle\frac{1}{n})\)
(\(\log\) の真数の積は和になるから)
\(=\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{2n}\log(2+\displaystyle\frac{k}{n})\)
ゆえに
\(\displaystyle\lim_{n \to \infty}\log b_n=\displaystyle\lim_{n \to \infty}\displaystyle\frac{1}{n}\displaystyle\sum_{k=1}^{2n}\log(2+\displaystyle\frac{k}{n})\)
\(=\displaystyle\int_{0}^{2}\log(2+x)dx\)
\(=[(2+x)\log(2+x)]_{0}^{2}-\displaystyle\int_{0}^{2}dx\)
\(=4\log4-2\log2-[x]_{0}^{2}\)
\(=4\log 4-\log 4-2\)
\(=3\log 4-2\log e\)
\(=\log4^3-\log e^2\)
\(=\log\displaystyle\frac{64}{e^2}\)
したがって
\(\displaystyle\lim_{n \to \infty}\log b_n=\log\displaystyle\frac{64}{e^2}\)
だから
\(\displaystyle\lim_{n \to \infty}b_n=\displaystyle\frac{64}{e^2}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→区分求積法③ back→区分求積法①