関数の大小と定積分の大小の関係について見ていきます。
・関数の大小と定積分の大小
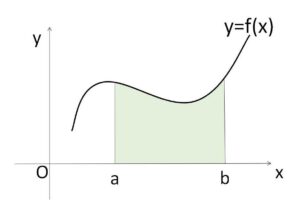
閉区間 \([a,b]\) で連続な関数\(f(x)\) が、この区間で常に \(f(x)≧0\) のとき、定積分が面積が表すことから次のことが成り立ちます。等号は、面積が\(0\)よりこの区間で常に \(f(x)=0\) のときに限り成立します。
\([a,b]\) で常に \(f(x)≧0\) ならば
\(\displaystyle\int_{a}^{b}f(x)dx≧0\)
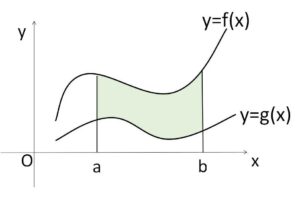
またこの定理を利用すると、閉区間 \([a,b]\) で連続な関数\(f(x),g(x)\)について次のことが成り立つことが分かります。等号は、この区間で常に \(f(x)=g(x)\) のときに限り成立します。
\([a,b]\) で常に \(f(x)≧g(x)\) ならば
\(\displaystyle\int_{a}^{b}f(x)dx≧\displaystyle\int_{a}^{b}g(x)dx\)
つまり、関数の大小関係がそのまま定積分の大小関係になります。
(証明)
\(h(x)=f(x)-g(x)\) とおくと \(h(x)≧0\) だから
\(\displaystyle\int_{a}^{b}h(x)dx≧0\)
よって
\(\displaystyle\int_{a}^{b}\{f(x)-g(x)\}dx≧0\)
だから
\(\displaystyle\int_{a}^{b}f(x)dx≧\displaystyle\int_{a}^{b}g(x)dx\)
等号成立は区間で常に \(h(x)=0\) のとき、つまり 常に \(f(x)=g(x)\) のとき。
なお、上図では\(f(x),g(x)\)がともに正であるような位置になっていますが、別に負でも構いません。
そして2つ目の定理から、次のことが成り立つことも分かります。
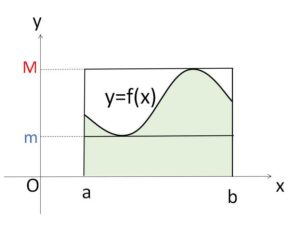
閉区間\([a,b]\)で連続な関数\(f(x)\)について、この区間での最小値と最大値をそれぞれ\(m,M\)とするとき
\(m(b-a)≦\displaystyle\int_{a}^{b}f(x)dx≦M(b-a)\)
(証明)
区間\([a,b]\)で常に \(m≦f(x)≦M\) だから
\(\displaystyle\int_{a}^{b}mdx≦\displaystyle\int_{a}^{b}f(x)dx≦\displaystyle\int_{a}^{b}Mdx\)
よって
\(m(b-a)≦\displaystyle\int_{a}^{b}f(x)dx≦M(b-a)\)
(例題)
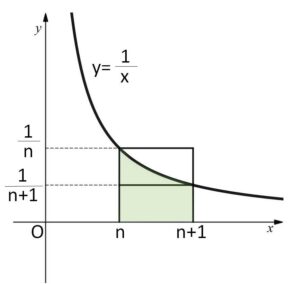
(1)自然数\(n\)に対して、\(\displaystyle\int_{n}^{n+1}\displaystyle\frac{1}{x}dx\) を求めよ。また、
\(\displaystyle\frac{1}{n+1}<\log(n+1)-\log n<\displaystyle\frac{1}{n}\)
を示せ。
(2)\(2\)以上の自然数\(n\)に対して
\(\log(n+1)<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k}<1+\log n\)
を示せ。
(3)\(2\)以上の自然数\(n\)に対して
\(\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{ee^{\frac{1}{2}}e^{\frac{1}{3}}\cdots e^{\frac{1}{k}}}>\displaystyle\frac{1}{e}\log(n+1)\)
を示せ。
(解答)
(1)
\(\displaystyle\int_{n}^{n+1}\displaystyle\frac{1}{x}dx=[\log|x|]_{n}^{n+1}\)
\(=\log(n+1)-\log n\)
また \(n≦x≦n+1\) のとき
\(\displaystyle\frac{1}{n+1}≦\displaystyle\frac{1}{x}≦\displaystyle\frac{1}{n}\)・・・①
①の等号は常には成立しないので
\(\displaystyle\int_{n}^{n+1}\displaystyle\frac{1}{n+1}dx<\displaystyle\int_{n}^{n+1}\displaystyle\frac{1}{x}dx<\displaystyle\int_{n}^{n+1}\displaystyle\frac{1}{n}dx\)
よって
\(\displaystyle\frac{1}{n+1}\displaystyle\int_{n}^{n+1}dx<\displaystyle\int_{n}^{n+1}\displaystyle\frac{1}{x}dx<\displaystyle\frac{1}{n}\displaystyle\int_{n}^{n+1}dx\)
となるから
\(\displaystyle\frac{1}{n+1}<\log(n+1)-\log n<\displaystyle\frac{1}{n}\)
(2)
(1)より、\(k\)を自然数として
\(\displaystyle\frac{1}{k+1}<\log(k+1)-\log k<\displaystyle\frac{1}{k}\)・・・②
②の左側の不等式で、\(k=1,2,\cdots,n-1\) として辺々加えると (目的の不等式に近づけるために\(n-1\)まで加える。この\(n-1\)があるので、\(n≧2\) の条件がついている)
\(\displaystyle\sum_{k=1}^{n-1}\displaystyle\frac{1}{k+1}<\displaystyle\sum_{k=1}^{n-1}\{\log(k+1)-\log k\}\)
よって
\(\displaystyle\sum_{k=2}^{n}\displaystyle\frac{1}{k}<\log n-0\)
両辺に\(1\)を加えて
\(\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k}<1+\log n\)
また、②の右側の不等式で、\(k=1,2,\cdots,n\) として辺々加えると
\(\displaystyle\sum_{k=1}^{n}\{\log(k+1)-\log k\}<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k}\)
よって
\(\log(n+1)<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k}\)
したがって
\(\log(n+1)<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k}<1+\log n\) (\(n≧2\))
が成り立つ。
(面積だと)
右上と左下の短冊は同じ面積です(ズレているだけ)。
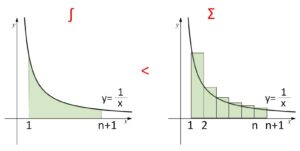
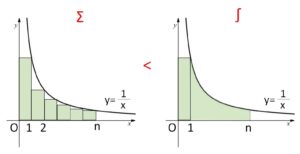
(3)
なので、(2)の不等式を使えばうまくいきそうです。最初に右左のどちらを使うかは、目的の不等式では逆数になっていることを考慮すると、右側になることが分かります。
(2)の右側の不等式より、\(k≧2\) のとき
\(1+\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}+\cdots+\displaystyle\frac{1}{k}<1+\log k\)
だから
\(ee^{\frac{1}{2}}e^{\frac{1}{3}}\cdots e^{\frac{1}{k}}=e^{1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{k}}<e^{1+\log k}=e\cdot e^{\log k}=ek\)
よって逆数をとると、\(k=1\) のときも含めて
\(\displaystyle\frac{1}{ee^{\frac{1}{2}}e^{\frac{1}{3}}\cdots e^{\frac{1}{k}}}≧\displaystyle\frac{1}{ek}\) (等号は \(k=1\) のときのみ成立)
\(k=1\) から \(k=n\) まで変化させて辺々加えると
\(\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{ee^{\frac{1}{2}}e^{\frac{1}{3}}\cdots e^{\frac{1}{k}}}>\displaystyle\frac{1}{e}\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k}\)・・・③
したがって③と(2)の左側の不等式
\(\log(n+1)<\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{k}\)
より
\(\displaystyle\sum_{k=1}^{n}\displaystyle\frac{1}{ee^{\frac{1}{2}}e^{\frac{1}{3}}\cdots e^{\frac{1}{k}}}>\displaystyle\frac{1}{e}\log(n+1)\) (\(n≧2\))
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→定積分と不等式②(三角形・台形近似) back→区分求積法③