回転体の体積を求めるやや発展的な問題について見ていきます。
(例題1)
2つの曲線
\(y=x^2-4x+3\), \(y=-x^2+2x-1\)
で囲まれた部分を、\(x\)軸の周りに1回転してできる立体の体積を求めよ。
今回は積分区間でどちらの関数の値も同じ符号(負)になるので、差をとるケースです。
(大きい方の回転体から中身をくり抜くケース)
(解答)
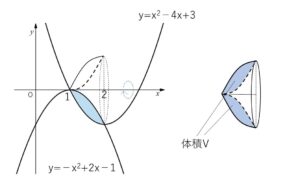
\(x^2-4x+3=-x^2+2x-1\) を解くと
\(x^2-3x+2=0\)
\((x-1)(x-2)=0\)
\(x=1,2\)
よって図から回転体の体積\(V\)は
\(V=π\displaystyle\int_{1}^{2}(x^2-4x+3)^2dx-π\displaystyle\int_{1}^{2}(-x^2+2x-1)^2dx\)
\(=π\displaystyle\int_{1}^{2}\{(x^2-4x+3)^2-(-x^2+2x-1)^2\}dx\)
\(=π\displaystyle\int_{1}^{2}\{(-2x+2)(2x^2-6x+4)\}dx\) (\(A^2-B^2=(A+B)(A-B)\))
\(=4π\displaystyle\int_{1}^{2}(-x^3+4x^2-5x+2)dx\)
\(=4π\left[-\displaystyle\frac{1}{4}x^4+\displaystyle\frac{4}{3}x^3-\displaystyle\frac{5}{2}x^2+2x\right]_{1}^{2}\)
\(=4π\left\{(-4+\displaystyle\frac{32}{3}-10+4)-(-\displaystyle\frac{1}{4}+\displaystyle\frac{4}{3}-\displaystyle\frac{5}{2}+2)\right\}\)
\(=\displaystyle\frac{1}{3}π\)
くり抜き型の体積の積分計算は
\(V=π\displaystyle\int_{α}^{β}[\{f(x)\}^2-\{g(x)\}^2]dx\)
と2乗の差を計算します。差の2乗 \(\{f(x)-g(x)\}^2\) ではありません。
(例題2)
放物線 \(y=x^2-3\) と 直線 \(y=2x\) で囲まれた図形を\(x\)軸の周りに回転してできる立体の体積を求めよ。
符号が反対の場合は、絶対値の大きいほうが優先される(小さい方はその内側に含まれることになる)のですが、手っ取り早い方法としてどうせ回転させるので、すべて正のほうにくるようにグラフを\(x\)軸について折り返す方法があります。そうすればくり抜き型に帰着できます。
(解答)
囲まれた図形を正の領域にくるように、\(x\)軸について折り返して考える。
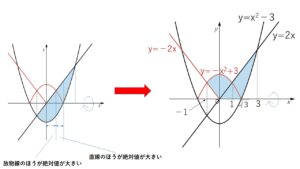
「\([-1,1]\)の放物線の積分、\([1,3]\)の直線の積分」から
「\([-1,0]\)の直線の積分、\([\sqrt{3},3]\)の放物線の積分」の2つの部分をくり抜きます。
求める体積\(V\)は
\(V=π\displaystyle\int_{-1}^{1}(-x^2+3)^2dx+π\displaystyle\int_{1}^{3}(2x)^2dx\)
\(-π\displaystyle\int_{-1}^{0}(-2x)^2dx-\displaystyle\int_{\sqrt{3}}^{3}(x^2-3)^2dx\)
それぞれの積分を計算すると
\(\displaystyle\int_{-1}^{1}(-x^2+3)^2dx\)
\(=\displaystyle\int_{-1}^{1}(x^4-6x^2+9)dx\)
\(=2\left[\displaystyle\frac{1}{5}x^5-2x^3+9x\right]_{0}^{1}\)
\(=\displaystyle\frac{72}{5}\)
\(\displaystyle\int_{1}^{3}(2x)^2dx\)
\(=\displaystyle\int_{1}^{3}4x^2dx\)
\(=\left[\displaystyle\frac{4}{3}x^3\right]_{1}^{3}\)
\(=\displaystyle\frac{104}{3}\)
\(\displaystyle\int_{-1}^{0}(-2x)^2dx\)
\(=\left[\displaystyle\frac{4}{3}x^3\right]_{-1}^{0}\)
\(=\displaystyle\frac{4}{3}\)
\(\displaystyle\int_{\sqrt{3}}^{3}(x^2-3)^2dx\)
\(=\left[\displaystyle\frac{1}{5}x^5-2x^3+9x\right]_{\sqrt{3}}^{3}\)
\(=\displaystyle\frac{108}{5}-\displaystyle\frac{24\sqrt{5}}{5}\)
よって
\(V=\displaystyle\frac{72}{5}π+\displaystyle\frac{104}{3}π-\displaystyle\frac{4}{3}π-(\displaystyle\frac{108}{5}-\displaystyle\frac{24\sqrt{5}}{5})π\)
\(=\displaystyle\frac{392+72\sqrt{3}}{15}π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→回転体の体積①