逆関数と面積の例題です。
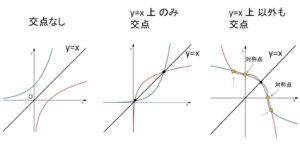
もとの関数と 直線 \(y=x\) が交点をもつならば、逆関数ともとの関数は交点をもち、しかも交点が \(y=x\) 上にあるので、このことに着目するのが大半です。
しかし、もとの関数自身に \(y=x\) について対称な点がある場合には、\(y=x\) 上以外にも交点をもつこともあるので、注意が必要です。
(例題1)
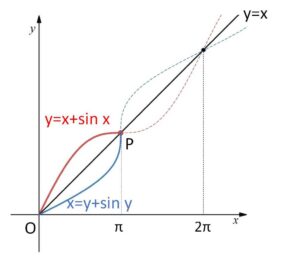
曲線 \(y=x+\sin x\) と 曲線 \(x=y+\sin y\) の第1象限の部分を考える。
(1)第1象限にあるこの2曲線の交点のうち原点\(O\)に最も近い交点\(P\)の座標を求めよ。
(2)この2曲線の\(O,P\)の間にある部分で囲まれる図形の面積を求めよ。
そして \(y=x+\sin x\) 自身に対称点がないことを調べます。
なお、\(y=x+\sin x\) のグラフは微分することで簡単に概形が分かります。
(解答)
(1)
2曲線のグラフは \(y=x\) について対称なので、交点をもつならば \(y=x\) 上にあるものが存在する。
\(y=x+\sin x\)・・・①
\(y=x\)・・・②
①②より
\(x+\sin x=x\)
\(\sin x=0\)・・・③
\(x>0\) において③を満たすのは
\(x=π,2π,\cdots\)
したがって \(0<x≦π\) の範囲で考えればよい。
このとき
\((x+\sin x)-x=\sin x≧0\)
だから、\(0<x<π\) では①は②の上側にあるので、2曲線のグラフは \(y=x\) 上以外で交わることはない。
したがって原点に最も近い交点の\(x\)座標は \(x=π\) だから、交点\(P\)の座標は
\(P(π,π)\)
(2)
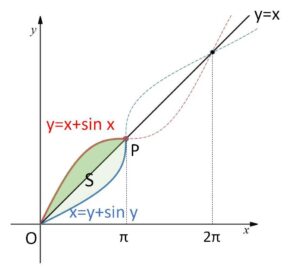
求める面積を\(S\)とすると、囲まれた図形は \(y=x\) について対称だから
\(\displaystyle\frac{S}{2}=\displaystyle\int_{0}^{π}(x+\sin x-x)dx\)
\(=[-\cos x]_{0}^{π}\)
\(=2\)
よって
\(S=4\)
(例題2)
(1)方程式 \(\displaystyle\frac{e^{x}-1}{e-1}-x=0\) の実数解は \(0,1\) のみであることを証明せよ。
(2)関数 \(y=\displaystyle\frac{e^{x}-1}{e-1}\) のグラフと、その逆関数のグラフとで囲まれる図形の面積を求めよ。
(解答)
(1)
より指数関数です。これと \(y=x\) 上の交点の\(x\)座標が方程式の解になりますが、指数関数は下に凸なので、直線 \(y=x\) との交点は多くても2個です。これらのことを記載してもよいですが、丁寧にやるなら微分して証明です。
(方程式を直接は解くことができないので、このような手法をとります)
\(f(x)=\displaystyle\frac{e^{x}-1}{e-1}-x\) とおく。
\(f'(x)=\displaystyle\frac{e^{x}}{e-1}-1\)
\(=\displaystyle\frac{e^x-(e-1)}{e-1}\)
\(e^x=e-1\) を満たすのは
\(x=\log(e-1)=α\) であり、\(0<α<1\)
(\(e^0<e-1<e^1\) より)
\(f(x)\)は
\(x≦α\) で単調減少、\(x≧α\) で単調増加。
また
\(f(0)=0\)、\(f(1)=1\) だから
\(y=f(x)\) のグラフは次のようになる。
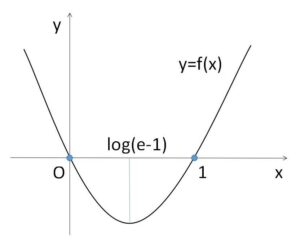
したがって \(f(x)=0\) の実数解は \(x=0,1\) のみである。
(2)
もとの指数関数と \(y=x\) の交点は(1)より2つで、交点の\(x\)座標は \(x=0,1\) と判明しています。他にもとの関数と逆関数で交点がないことは、\(x<0,\ 0<x<1,\ x>1\) で3分割して上下関係を考えればわかります。
面積は(例題1)と同様に半分の部分を考えて2倍します。
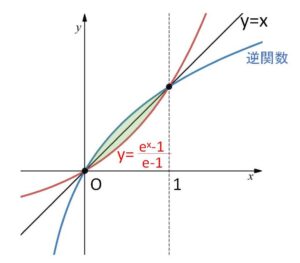
(1)より
\(y=\displaystyle\frac{e^x-1}{e-1}=g(x)\) と \(y=x\) のグラフの交点は\(2\)つで、その\(x\)座標は \(x=0,1\)。
\(x<0\)、\(x>1\) のとき \(g(x)>x\)
\(0<x<1\) のとき \(g(x)<x\)
だから \(y=g(x)\) と逆関数の交点は \(y=x\) 上以外には存在しない。・・・(注)
よって囲まれた図形の面積\(S\)は、図形が \(y=x\) について対称となることから
\(\displaystyle\frac{S}{2}=\displaystyle\int_{0}^{1}\left(x-\displaystyle\frac{e^{x}-1}{e-1}\right)dx\)
\(=\left[\displaystyle\frac{x^2}{2}-\displaystyle\frac{e^x-x}{e-1}\right]_{0}^{1}\)
\(=\displaystyle\frac{1}{2}-\displaystyle\frac{(e-1)-1}{e-1}\)
\(=\displaystyle\frac{(e-1)-2(e-2)}{2(e-1)}\)
\(=\displaystyle\frac{3-e}{2(e-1)}\)
したがって
\(S=\displaystyle\frac{3-e}{e-1}\)
(注)
逆関数も関数なので、\(0<x<1\) の区間で \(y=\displaystyle\frac{e^{x}-1}{e-1}\) を \(y=x\) について折り返すと、折り返したグラフ(逆関数のグラフ)はこの区間からはみ出ることはありません。他の区間でも同様なので、\(y=x\) 上以外に交点が存在しないことになります。(例題1)では説明を省きましたが、同様の議論となります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→極座標と面積 back→極限と面積