\(y\)軸方向の積分による面積計算について見ていきます。
・\(y\)軸方向の積分と面積
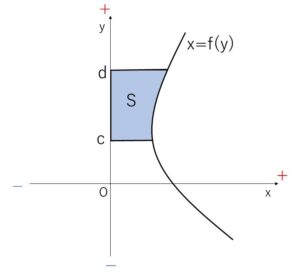
\(y\)軸をあたかも\(x\)軸のように見ると、曲線 \(x=f(y)\) と \(y=c\)、\(y=d\) (\(c<d\)) で囲まれた面積\(S\)は次のような定積分で求めることができます。
\(S=\displaystyle\int_{c}^{d}|f(y)|dy\)
2曲線で囲まれた面積についても同様で、2曲線 \(x=f_1(y)\)、\(x=f_2(y)\) と \(y=c\)、\(y=d\) (\(c<d\)) で囲まれた面積\(S\)は
\(S=\displaystyle\int_{c}^{d}|f_1(y)-f_2(y)|dy\)
となります。
\(x=f(y)\) の形で曲線の方程式が与えられている場合は上記の積分をすればよいのですが、\(y=g(x)\) (\(y=(xの式)\)) で与えられている場合には、
①\(x=f(y)\) の式にできるならば変形する(逆関数を求める)
ことが第1手段ですが、それが困難な場合には
②置換積分を利用する
③座標平面図から図形の組み合わせで求める
(いずれも\(x\)軸方向の定積分を活用することなる)
ことになります。
逆も然りで \(x=f(y)\) の形で曲線の式が与えられている場合に、この曲線と\(x\)軸との間の図形の面積を求める場合にも同様の手順を踏むことになります。
また、\(y=g(x)\) の形で曲線の式が与えられていて、この曲線と\(x\)軸との間の図形の面積を求める場合には通常は \(\displaystyle\int_{a}^{b}g(x)dx\) の計算をしますが、この積分が面倒な場合には敢えて\(y\)軸方向の積分に変換すると楽になる場合もあります。
いずれにせよ、\(x,y\)軸方向の一方の積分では面倒な場合にはもう一方の変数の積分にシフトチェンジするという考えた方が重要になります。
(例題)
曲線 \(y=\log x\) と \(x\)軸、\(y\)軸、\(y=\log2\) で囲まれる図形の面積\(S\)を求めよ。
(解答1)\(x=f(y)\)の式にする
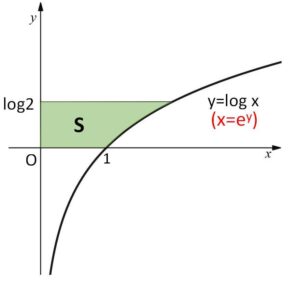
\(y=\log x\) より \(x=e^{y}\) だから
\(S=\displaystyle\int_{0}^{\log2}e^ydy\)
\(=[e^{y}]_{0}^{\log2}\)
\(=e^{\log2}-1\)
\(=2-1\)
\(=1\)
(解答2)置換積分を利用
\(S=\displaystyle\int_{0}^{\log 2}xdy\)
であり、\(y\)を消去するような意識で置換積分を行います。
\(y=\log x\) より
\(dy=\displaystyle\frac{1}{x}dx\)
また、\(y:0 \to \log2\) のとき \(x:1 \to 2\) だから
\(S=\displaystyle\int_{0}^{\log 2}xdy\)
\(=\displaystyle\int_{1}^{2}x\cdot\displaystyle\frac{1}{x}dx\)
\(=\displaystyle\int_{1}^{2}dx\)
\(=2-1\)
\(=1\)
(解答3)面積を組み合わせて求める
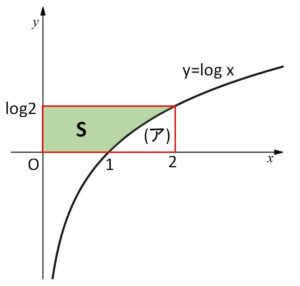
\(S\)は長方形から図形(ア)を除いた部分の面積だから
\(S=2×\log2-\displaystyle\int_{1}^{2}\log xdx\)
(積分は部分積分をする。もしくは\(\log x\)の積分公式より直接計算してもよい)
\(=2\log2-[x\log x]_{1}^{2}+\displaystyle\int_{1}^{2}x\cdot\displaystyle\frac{1}{x}dx\)
\(=2\log2-2\log2+\displaystyle\int_{1}^{2}dx\)
\(=2-1\)
\(=1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→接線と面積 back→2曲線で囲まれる面積②