媒介変数表示された曲線で囲まれる面積を求める例題です。
①媒介変数を消去する
②概形を描いて、置換積分をする
になります。消去可能な場合は①②どちらでも解くことができますが、消去不可の場合には②のみになります。よって②のほうが重要度は高いです。
②の解法で解く場合には、特に気を付けるのが\(x\)軸方向で積分する場合に、\(y\)が\(x\)の関数になっているか(\(x\)1つに対して\(y\)が2個以上ないか)の確認です。これは\(x\)の媒介変数\(t\)による微分 \(\displaystyle\frac{dx}{dt}\) を調べれば分かります。単調増加(減少)になれば、\(t\)を変化させたときに曲線が横方向に戻ることが無いので、関数であることがいえます。もし単調増加(減少)にならない場合には、分割して求めることになります(これらの概形を描くとすぐに分かる)。
\(y\)の増減については特に気にしなくてよいですが、正負だけには注意します。
(例題1)
媒介変数\(θ\)を用いて表された曲線
\(x=2\sqrt{2}\cosθ\)、\(y=\displaystyle\frac{1}{2}\sin2θ\) (\(0≦θ≦\displaystyle\frac{π}{2}\))
がある。この曲線と\(x\)軸とで囲まれた部分の面積を求めよ。
面積計算は置換積分を利用します。
\(x=2\sqrt{2}\cosθ\)、\(y=\displaystyle\frac{1}{2}\sin2θ\) (\(0≦θ≦\displaystyle\frac{π}{2}\))
\(\displaystyle\frac{dx}{dθ}=-2\sqrt{2}\sinθ\ (≦0)\)
\(\displaystyle\frac{dy}{dθ}=\cos2θ\)
よって増減表とグラフは次の通り。
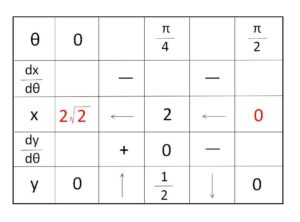
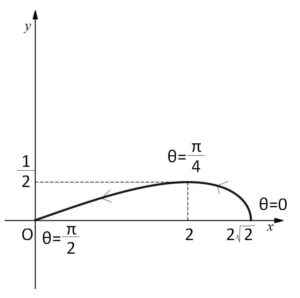
したがって面積\(S\)は、\(dx=-2\sqrt{2}\sinθdθ\) だから
\(S=\displaystyle\int_{0}^{2\sqrt{2}}ydx\)
\(=\displaystyle\int_{\frac{π}{2}}^{0}\displaystyle\frac{1}{2}\sin2θ(-2\sqrt{2}\sinθdθ)\) (積分区間も対応する\(θ\)にする)
\(=\sqrt{2}\displaystyle\int_{0}^{\frac{π}{2}}\sin2θ\sinθdθ\)
(2倍角の公式より、導関数接触型にする。または積和でもよい。)
\(=2\sqrt{2}\displaystyle\int_{0}^{\frac{π}{2}}\sin^2θ\cosθdθ\)
\(=2\sqrt{2}\left[\displaystyle\frac{1}{3}\sin^3θ\right]_{0}^{\frac{π}{2}}\)
\(=\displaystyle\frac{2\sqrt{2}}{3}\)
※\(x\)の単調性に着目すると
\(x=2\sqrt{2}\cosθ\) (\(0≦x≦\displaystyle\frac{π}{2}\)) だから
\(\displaystyle\frac{dx}{dθ}=-2\sqrt{2}\sinθ\) より、\(x\)は単調減少。よってこの曲線は全体として\(x\)の関数となる。また、\(y=\displaystyle\frac{1}{2}\sin2θ≧0\) で、\(x\)軸との交点の\(x\)座標は、\(y=0\) より \(θ=0,\displaystyle\frac{π}{2}\) のときを考えて、\(x=2\sqrt{2},0\)。以上のことから面積\(S\)は \(S=\displaystyle\int_{0}^{2\sqrt{2}}ydx\) となるので、あとは同様に置換積分をすればよいことになる。こうすればやや手間は省ける。
※媒介変数を消去すると
\(x=2\sqrt{2}\cosθ\)・・・①
\(y=\displaystyle\frac{1}{2}\sin2θ\)・・・② (\(0≦θ≦\displaystyle\frac{π}{2}\))
\(\sinθ≧0\) だから①より
\(\sinθ=\sqrt{1-\cos^2θ}=\sqrt{1-\displaystyle\frac{x^2}{8}}\)
よって②より
\(y=\sinθ\cosθ\) だから
\(y=\displaystyle\frac{1}{2\sqrt{2}}\cdot x\sqrt{1-\displaystyle\frac{x^2}{8}}\)
定義域は①より
\(0≦x≦2\sqrt{2}\)
\(y≧0\) なので、あとはそのまま積分すればよい。
(例題2)
曲線
\(\begin{eqnarray} \left\{ \begin{array}{l} x = t^2 \\ y = 2+t-t^2 \end{array} \right. \end{eqnarray}\) (\(-\infty<t<\infty\))
と\(x\)軸とで囲まれた部分の面積を求めよ。
\(\begin{eqnarray} \left\{ \begin{array}{l} x = t^2 \\ y = 2+t-t^2 \end{array} \right. \end{eqnarray}\) (\(-\infty<t<\infty\))
\(\displaystyle\frac{dx}{dt}=2t\)
\(\displaystyle\frac{dy}{dt}=1-2t\)
また、\(2+t-t^2=0\) を満たすのは
\((t+1)(t-2)=0\) より \(t=-1,2\) だから
曲線と\(x\)軸の交点の\(x\)座標は、\(x=1,4\)
また \(x=α\ (>0)\) のとき \(t=±\sqrt{α}\) でありこれを\(y\)の式に代入すると
\(y=2+\sqrt{α}-α,\ 2-\sqrt{α}-α\)
\(2+\sqrt{α}-α> 2-\sqrt{α}-α\) だから、曲線は自身で交わることは無い。・・・(注)
以上のことと、増減表よりグラフは次のようになる。
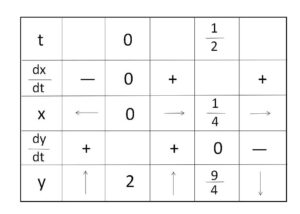
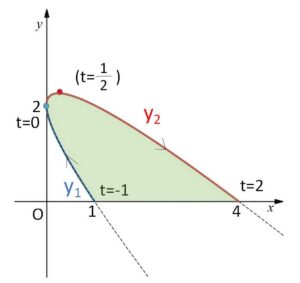
したがって求める面積\(S\)は、\(dx=2tdt\) だから
(2つの関数\(y_1,y_2\)に分けて、置換積分をします)
\(S=\displaystyle\int_{0}^{4}y_2dx-\displaystyle\int_{0}^{1}y_1dx\)
(対応する\(t\)の値には注意する。被積分関数は同じになる。)
\(=\displaystyle\int_{0}^{2}(2+t-t^2)\cdot2tdt-\displaystyle\int_{0}^{-1}(2+t-t^2)\cdot2tdt\)
\(=\displaystyle\int_{0}^{2}(4t+2t^2-2t^3)dt+\displaystyle\int_{-1}^{0}(4t+2t^2-2t^3)dt\)
(積分区間がつながっているので)
\(=\displaystyle\int_{-1}^{2}(4t+2t^2-2t^3)dt\)
\(=\left[2t^2+\displaystyle\frac{2}{3}t^3-\displaystyle\frac{1}{2}t^4\right]_{-1}^{2}\)
\(=(8+\displaystyle\frac{16}{3}-8)-(2-\displaystyle\frac{2}{3}-\displaystyle\frac{1}{2})\)
\(=\displaystyle\frac{9}{2}\)
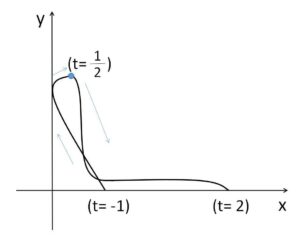
(注)について
増減表だけだと、\(t≧\displaystyle\frac{1}{2}\) で曲線が自身で交わる可能性を否定できない(下図参照)。そのため \(x=α\) のときに2つの\(y\)が一致しないことの確認をしました(大小も分かった)。
※媒介変数を消去する方法だと
\(\begin{eqnarray} \left\{ \begin{array}{l} x = t^2・・・① \\ y = 2+t-t^2・・・② \end{array} \right. \end{eqnarray}\) (\(-\infty<t<\infty\))
①より \(x≧0\) でこのとき
\(t=±\sqrt{x}\)
これを②に代入すると
\(y=2±\sqrt{x}-x\)
あとは概形を調べて積分すればよい。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→媒介変数と面積②(トロコイド・サイクロイド) back→陰関数と面積