空間における平面図形の回転体の体積を求める例題です。
今回は回転前の断面は線分になります。線分を回転させるという一見ややこしい操作をしますが、線分が点の集まりであることを考えて1点1点の回転を考えれば、それぞれは円を描くことになり、そこまで難しくはありません。
(例題)
\(xyz\)空間に3点\(P(1,1,0)\)、\(Q(-1,1,0)\)、\(R(-1,1,2)\) をとる。
(1)\(t\)を \(0<t<2\) を満たす実数とするとき、平面 \(z=t\) と、\(△PQR\)の交わりに現れる線分の2つの端点の座標を求めよ。
(2)\(△PQR\)を\(z\)軸の周りに回転して得られる回転体の体積を求めよ。
(解答)
(1)
\(△PQR\)は\(xz\)平面に平行で、しかも\(QR\)は\(z\)軸に平行、\(QP\)は\(x\)軸に平行なので分かりやすい形をしています。(これより\(QR\)上の交点の\(x,y\)座標は\(Q,R\)と同じであることなどがすぐに分かる)
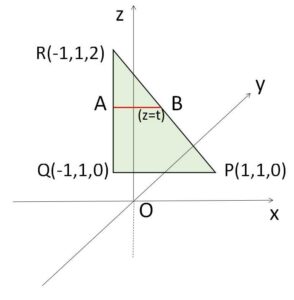
線分\(QR,PR\) と平面 \(z=t\) の交点をそれぞれ\(A,B\)とする。\(A,B\)の座標が求めるものである。
まず\(A\)について、\(0≦k≦1\) とすると
\(\overrightarrow{OA}=\overrightarrow{OQ}+k\overrightarrow{QR}\)
\(=(-1,1,0)+k(0,0,2)\)
\(=(-1,1,2k)\)
\(2k=t\) より、\(A\)の座標は
\(A(-1,1,t)\)
同様に\(B\)について
\(\overrightarrow{OB}=\overrightarrow{OP}+k\overrightarrow{PR}\)
\(=(1,1,0)+k(-2,0,2)\)
\(=(1-2k,1,2k)\)
\(2k=t\) より \(B\)の座標は
\(B(1-t,1,t)\)
(2)
ここで1つ注意です。 \(z=t\) 上 (\(xy\)平面に平行な平面上) において、\(A\)は定点、\(B\)は\(y\)座標は固定で\(x\)座標は変化します(\(0<t<2\) で変化させると、\(B\)は\((1,1)\)から\((-1,1)\) まで動く)。したがってこの例題では原点から直線\(AB\)に垂線を下ろすときに垂線の足が線分\(AB\)上に存在する場合と存在しない場合があります。よって一番近い点については\(t\)の値によって場合分けする必要があります。一番遠い点については常に\(A\) (\(t=0\) のときは\(A\)と\(B\)) になります。
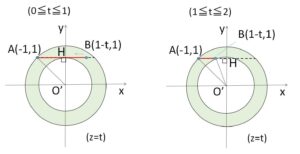
回転体を \(z=t\) で切断したときの断面を\(S(t)\)とする。
\(O'(0,0,t)\) から直線\(AB\)に下した垂線の足を\(H\)とすると、\(H\)の\(x\)座標は\(0\)である。
(i)\(0≦t≦1\) のとき・・・(注1)
\(H\)は線分\(AB\)上に存在するので
\(S(t)=π(O’A^2-O’H^2)=π(2-1)=π\)・・・(注2)
(ii)\(1≦t≦2\) のとき・・・(注1)
\(S(t)=π(O’A^2-O’B^2)\)
\(=π\{2-(1-t)^2-1\}\)
\(=π(2t-t^2)\)
よって体積\(V\)は
\(V=\displaystyle\int_{0}^{1}πdt+\displaystyle\int_{1}^{2}π(2t-t^2)dt\)
\(=π[t]_{0}^{1}+π\left[t^2-\displaystyle\frac{1}{3}t^3\right]_{1}^{2}\)
\(=π+π(3-\displaystyle\frac{7}{3})\)
\(=\displaystyle\frac{5}{3}π\)
(注1)
\(t=0,2\)は(1)の範囲に含まれていませんが、まとめて扱いました。
\(t=0\) のときは特に問題なく、\(t=2\) のときは\(A,B\)は一致するだけで、(1)の座標がそのまま使えます。
(注2)
\(0≦t≦1\) のときは結局、線分の左部分\(HA\)だけを考えていることになります。右部分\(HB\)については\(HA\)を回転してできる領域に全部含まれます。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→立体の回転③(空間図形の回転) back→空間の回転①(線分の回転)