図形が通過してできる立体の体積を求める問題です。
(例題1)
\(xyz\)空間に、\(xy\)平面の原点を中心とする半径\(1\)の円板\(F\)がある。2点 \(A(0,0,1),B(1,0,1)\) を結ぶ線分\(AB\)上に点\(P\)をとり、\(P\)を頂点とし\(F\)を底面とする円錐を考える。\(P\)を\(A\)から\(B\)まで動かすとき、このような円錐全体でつくられる立体を\(K\)とする。
(1)平面 \(z=h\) (\(0<h<1\)) で\(K\)を切った切り口の面積\(S(h)\)を求めよ。
(2)\(K\)の体積\(V\)を求めよ。
(解答)
(1)
(\(P\)を1つ固定して断面を考えて、あとで動かすという方針をとります)
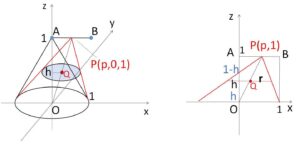
\(P(p,0,1)\) (\(0≦p≦1\)) とおく。
\(P\)を固定したときの円錐の \(z=h\) による断面は円であり、その中心\(Q\)は線分\(OP\)を \(h:1-h\) に内分する点だから
\(Q(hp,0,h)\)
この円の半径\(r\)は、\(1:r=1:1-h\) より
\(r=1-h\)
よって、\(z=h\) におけるこの円の方程式は
\((x-hp)^2+y^2=(1-h)^2\)
\(p\) を \(0≦p≦1\) の範囲で動かすとこの円は\(x\)軸に平行に動くので、立体\(K\)の \(z=h\) の断面は次のようになる。
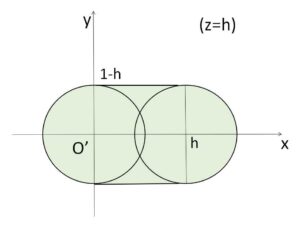
したがって断面積は
\(S(h)=π(1-h)^2+2(1-h)h\)
(参考)ベクトルを利用すると
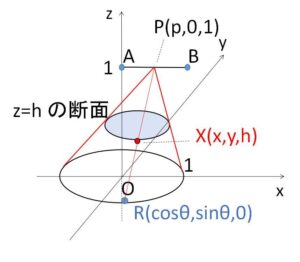
円錐の頂点を \(P(p,0,1)\)、底面の円周上の点を \(R(\cosθ,\sinθ,0)\) とおく。
線分\(PR\)上の点\(X\)とすると、\(0≦k≦1\) として
\(\overrightarrow{OX}=\overrightarrow{OP}+k\overrightarrow{PR}\)
\(=(p,0,1)+k(\cosθ-p,\sinθ,-1)\)
\(=(p+k(\cosθ-p),\ k\sinθ,\ 1-k)\)
\(X\)の\(z\)座標を\(h\)、つまり \(X(x,y,h)\) とすると
\(1-k=h\) よって \(k=1-h\)
ゆえに
\(X(p+(1-h)(\cosθ-p),\ (1-h)\sinθ,\ h)\) となるから
\(x=(1-h)\cosθ+ph\)・・・①
\(y=(1-h)\sinθ\)・・・②
したがって ①②より \(z=h\) 上において \(X(x,y)\) は 中心\((ph,0)\)、半径\((1-h)\) の円を描くことが分かる。(実際①②から\(θ\)を消去すれば方程式が求まる)
つまり断面は円になる。
また、\(Q(ph,0,h)\) とおくと、
\(\overrightarrow{OQ}=h\overrightarrow{OP}\) (\((ph,0,h)=h(p,0,1)\))
となることから、\(OP\)上に断面の円の中心\(Q\)があることも分かる。
(2)
(積分するだけです)
(1)の\(S(t)\)は、\(h=0,1\)のときも成り立つから、体積\(V\)は
\(V=\displaystyle\int_{0}^{1}\{π(1-h)^2+2h-2h^2\}dh\)
\(=\left[\displaystyle\frac{-π(1-h)^3}{3}+h^2-\displaystyle\frac{2h^3}{3}\right]_{0}^{1}\)
\(=\displaystyle\frac{1}{3}+\displaystyle\frac{π}{3}\)
(例題2)
(1)平面上に1辺の長さ\(4\)の正三角形がある。\(r\)を\(1\)以下の正の実数とし、半径\(r\)の円の中心が、平面内でこの正三角形の辺上を1周するとき、この円が通過する部分の面積を求めよ。
(2)空間内に1辺の長さが\(4\)の正三角形があり、半径\(1\)の球の中心がこの三角形の周上を1周するとき、この球が通過する部分の体積を求めよ。
(解答)
(1)
面積は、正三角形の内側の部分と外側の部分で分けて求めます。
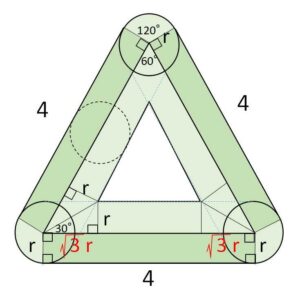
円の通過領域は上図のようになる。
3隅の扇形は合わせると円になり、空洞となっている正三角形の1辺は \(4-2\sqrt{3}r\) だから、面積\(S\)は
\(S=\left\{\displaystyle\frac{1}{2}\cdot4^2\cdot\sin\displaystyle\frac{π}{3}-\displaystyle\frac{1}{2}\cdot(4-2\sqrt{3}r)^2\cdot\sin\displaystyle\frac{π}{3}\right\}+3×4r+πr^2\)
\(=(12r-3\sqrt{3}r^2)+12r+πr^2\)
\(=24r+(π-3\sqrt{3})r^2\)
(2)
球の断面は円であり、球を正三角形のレールに沿って動かすとこの円が同じように平行移動するので、(1)の結果が利用できます。
正三角形を含む面を\(xy\)平面として、これに垂直に\(z\)軸をとる。
\(xyz\)空間の原点を中心とする半径\(1\)の球の方程式は
\(x^2+y^2+z^2=1\)
\(z=t\) (\(-1<t<1\)) による切り口の円の方程式は
\(x^2+y^2=1-t^2\)
よって円の半径は \(\sqrt{1-t^2}\) となる。
(\(t=±1\) のときは切り口は1点になる)
(1)の結果は \(r=0\) でも成り立つので、題意の立体の \(z=t\) による断面積は、(1)で \(r=\sqrt{1-t^2}\) として
\(S(t)=24\sqrt{1-t^2}+(π-3\sqrt{3})(1-t^2)\)
となるから求める体積\(V\)は
\(V=\displaystyle\int_{-1}^{1}\{24\sqrt{1-t^2}+(π-3\sqrt{3})(1-t^2)\}dt\)
\(=2\displaystyle\int_{0}^{1}\{24\sqrt{1-t^2}+(π-3\sqrt{3})(1-t^2)\}dt\)
(1項目の積分は\(\frac{1}{4}\)円)
\(=2\left\{24\cdot\displaystyle\frac{π}{4}+(π-3\sqrt{3})\left[t-\displaystyle\frac{1}{3}t^3\right]_{0}^{1}\right\}\)
\(=\displaystyle\frac{40}{3}π-4\sqrt{3}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→バウムクーヘン分割 back→立体の共通部分