空間における斜軸の回転体の体積を求める例題です。
また平面の斜軸回転体と同様に、軸方向の変数で積分することに注意します。軸方向に長さ\(t\)をとり\(t\)で積分する際には問題ないですが、これ以外の場合は置換積分により調整用の項を掛ける必要がでてきます。
(例題)
\(xyz\)空間の原点と点\((1,1,1)\)を通る直線を\(l\)とする。
(1)\(l\)上の点 \((\displaystyle\frac{t}{3},\displaystyle\frac{t}{3},\displaystyle\frac{t}{3})\) を通り\(l\)と垂直な平面が、\(xy\)平面と交わってできる直線の方程式を求めよ。
(2)不等式 \(0≦y≦x(1-x)\) の表す\(xy\)平面内の領域を\(D\)とする。\(l\)を軸として\(D\)を回転させて得られる回転体の体積を求めよ。
(解答)
(1)
平面の法線ベクトルは \((1,1,1)\) です。
\((\displaystyle\frac{t}{3},\displaystyle\frac{t}{3},\displaystyle\frac{t}{3})\) を通り\(l\)と垂直な平面の方程式は、法線ベクトルが \((1,1,1)\) であることから
\(1\cdot(x-\displaystyle\frac{t}{3})+1\cdot(y-\displaystyle\frac{t}{3})+1\cdot(z-\displaystyle\frac{t}{3})=0\)
整理して
\(x+y+z=t\)・・・①
平面①と\(xy\)平面の交わりでできる直線の方程式は、①で \(z=0\) として
\(x+y=t\) (\(z=0\))
(2)
(1)を利用することにすると、回転前の領域を平面①で切断した場合、領域\(D\)が\(xy\)平面上にしか存在しないことから、①による断面は領域\(D\)と直線 \(x+y=t\) の共通部分になります(両端以外は線分になる)。この線分上の点のうち、回転軸上の点 \(O'(\displaystyle\frac{t}{3},\displaystyle\frac{t}{3},\displaystyle\frac{t}{3})\) から最も近い点と遠い点を探すことになりますが、\(O’\)が\(xy\)平面上にないので直接考えるのは面倒です。この場合 \(O’\) から\(xy\)平面に垂線\(O’H\)を引いてワンクッションいれるとよいです。点と点の距離を計算する際に、\(z\)に関する2乗については断面の線分上ではどこでも共通で\(\displaystyle\frac{t^2}{9}\)なので、\(H\)との距離を調べればよいことになります。
回転軸\(l\)の\(xy\)平面への影は \(y=x\) であり、この直線上に\(H\)があります。よって\(y=x\)、 \(x+y=t\) に平行な直線、領域\(D\)の位置関係に注意しながら進めていきます。
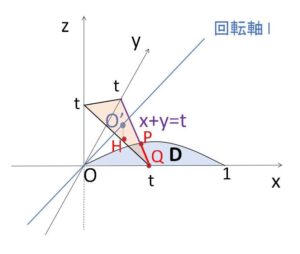
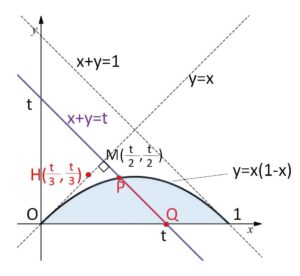
平面 \(x+y+z=t\)・・・① による断面を考える。
以下 \(y=x\)、\(x+y=1\) が、\(y=x(1-x)\) に接することに注意する。
回転させる前の断面は、\(x+y=t\)・・・② と領域\(D\)の共通部分であり、共通部分が存在するのは \(0≦t≦1\)。回転体の断面積を\(S\)とすると
(i)\(t=0,1\) のとき
共通部分は1点であるから \(S=0\)
(ii)\(0<t<1\) のとき
\(x+y=t\)・・・② 領域\(D\)の共通部分は線分\(PQ\)となる。
\(O'(\displaystyle\frac{t}{3},\displaystyle\frac{t}{3},\displaystyle\frac{t}{3})\) とおいて、\(O’\)から\(xy\)平面におろした垂線の足を\(H(\displaystyle\frac{t}{3},\displaystyle\frac{t}{3},0)\) とすると、\(H\)は直線②の下側にあり、\(y=x\) 上の点である。
線分\(PQ\)上にある点を\(X\)とすると
\(O’X^2=O’H^2+HX^2=\displaystyle\frac{t^2}{9}+HX^2\)
となるから、\(H\)から最も遠い(近い)点\(X\)が、\(O’\)から最も遠い(近い)点になる。
よって図の角\(M\)が直角であることから、\(O’\)から最も遠い点は\(Q\)、近い点は\(P\)となる。
ここで、\(x+y=t\)・・・② と \(y=x(1-x)\) から\(y\)を消去すると
\(t-x=x-x^2\)
\(x^2-2x+t=0\)
この2次方程式の解の小さいほうが\(P\)の\(x\)座標になるから、②も用いると
\(P(1-\sqrt{1-t},\ t-1+\sqrt{1-t})\) (\(z=0\))
ゆえに
\(S=πO’Q^2-πO’P\)
\(=π(O’H^2+HQ^2)-π(O’H^2+HP^2)\)
\(=πHQ^2-πHP^2\)
\(=π\left\{(\displaystyle\frac{2t}{3})^2+(\displaystyle\frac{t}{3})^2\right\}-π\left\{(1-\sqrt{1-t}-\displaystyle\frac{t}{3})^2+(1-\sqrt{1-t}-\displaystyle\frac{2t}{3})^2\right\}\)
\(=\displaystyle\frac{5}{9}πt^2-π\left\{2(1-\sqrt{1-t})^2-2t(1-\sqrt{1-t})+\displaystyle\frac{5}{9}t^2\right\}\)
\(=π\left\{-2(2-t-2\sqrt{1-t})+2t(1-\sqrt{1-t})\right\}\)
\(=π(-4+4t+4\sqrt{1-t}-2t\sqrt{1-t})\)・・・③
(③で\(t=0,1\)とすると、\(S=0\) となるので③は\(t=0,1\)のときも成り立つ)
または、\(t\)から\(t+Δt\) までの立体の高さの変化を考える方法もあります。(参考参照)
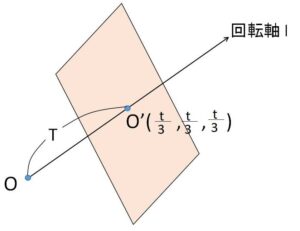
\(OO’\)方向に\(T\)座標軸を設定し、\(OO’=T\) とすると
\(T=\displaystyle\frac{1}{\sqrt{3}}t\)
したがって求める体積\(V\)は
\(V=\displaystyle\int_{0}^{\frac{1}{\sqrt{3}}}SdT\)
\(=\displaystyle\int_{0}^{1}π(-4+4t+4\sqrt{1-t}-2t\sqrt{1-t})\cdot\displaystyle\frac{1}{\sqrt{3}}dt\)
\(=\displaystyle\frac{π}{\sqrt{3}}\displaystyle\int_{0}^{1}(-4+4t+4\sqrt{1-t})dt-\displaystyle\frac{2π}{\sqrt{3}}\displaystyle\int_{0}^{1}t\sqrt{1-t}dt\)
(2つ目の積分は、\(1-t=u\) の置換をして)
\(=\displaystyle\frac{π}{\sqrt{3}}\left[-4t+2t^2-\displaystyle\frac{8}{3}(1-t)^{\frac{3}{2}}\right]_{0}^{1}-\displaystyle\frac{2π}{\sqrt{3}}\displaystyle\int_{1}^{0}(1-u)\sqrt{u}\cdot(-1)du\)
\(=\displaystyle\frac{π}{\sqrt{3}}\cdot\displaystyle\frac{2}{3}+\displaystyle\frac{2π}{\sqrt{3}}\displaystyle\int_{0}^{1}(u^{\frac{3}{2}}-u^{\frac{1}{2}})du\)
\(=\displaystyle\frac{2π}{3\sqrt{3}}+\displaystyle\frac{2π}{\sqrt{3}}\left[\displaystyle\frac{2}{5}u^{\frac{5}{2}}-\displaystyle\frac{2}{3}u^{\frac{3}{2}}\right]_{0}^{1}\)
\(=\displaystyle\frac{2π}{3\sqrt{3}}+\displaystyle\frac{2π}{\sqrt{3}}\cdot(-\displaystyle\frac{4}{15})\)
\(=\displaystyle\frac{2π}{15\sqrt{3}}\)
\(=\displaystyle\frac{2\sqrt{3}π}{45}\)
(参考)
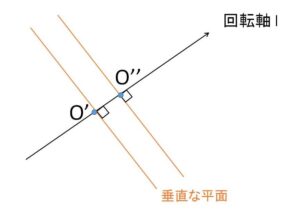
\(O'(\displaystyle\frac{t}{3},\displaystyle\frac{t}{3},\displaystyle\frac{t}{3})\) について、\(t\)を\(Δt\)だけ変化させたときの点を \(O”(\displaystyle\frac{t+Δt}{3},\displaystyle\frac{t+Δt}{3},\displaystyle\frac{t+Δt}{3})\) とすれば
\(O’O”=\sqrt{(\displaystyle\frac{Δt}{3})^2+(\displaystyle\frac{Δt}{3})^2+(\displaystyle\frac{Δt}{3})^2}=\displaystyle\frac{Δt}{\sqrt{3}}\)
これが、微小体積の高さになるので
\(V=\displaystyle\int_{0}^{1}S\cdot\displaystyle\frac{dt}{\sqrt{3}}\)
としてもよい。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→空間の斜軸回転体② back→バウムクーヘン分割