回転体の体積

\(x\)軸まわりの回転体の体積についてです。

・\(x\)軸まわりの回転体の体積

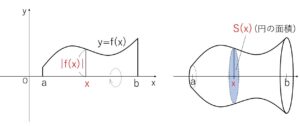
曲線 \(y=f(x)\) と\(x\)軸、2直線 \(x=a\)、\(x=b\) (\(a<b\)) で囲まれた図形を\(x\)軸まわりに1回転してできる立体の体積を\(V\)とします。
\((x,0)\)を通り\(x\)軸に垂直な平面で立体を切断したときの断面図は、上左図の長さ\(|f(x)|\)の線分の回転体を考えると半径\(|f(x)|\)の円になることが分かるので(回転してから切るのではなく回転する前に切るという重要な考え方)、その断面積\(S(x)\)は
\(S(x)=π\{f(x)\}^2=πy^2\)

よって立体の体積は次のようになります。
\(V=π\displaystyle\int_{a}^{b}\{f(x)\}^2dx=π\displaystyle\int_{a}^{b}y^2dx\)

(注)
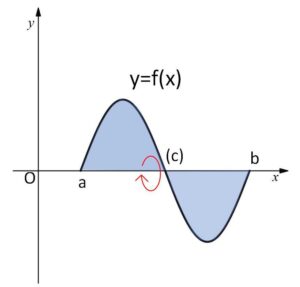
1つの関数の回転体の体積では、負の部分があっても上式になります。例えば下図の場合でも
\(V=π\displaystyle\int_{a}^{b}\{f(x)\}^2dx\)
\(\left(=π\displaystyle\int_{a}^{c}\{f(x)\}^2dx+π\displaystyle\int_{c}^{b}\{f(x)\}^2dx\right)\)

・2曲線で囲まれた図形の回転体

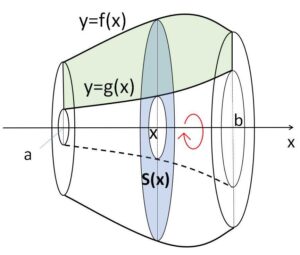
\(f(x),g(x)\)は同符号(注1)、\(|f(x)|≧|g(x)|\) とします。
\(f(x),g(x)≧0\) の場合を考えると(負の場合でも同じ)、2つの曲線 \(y=f(x)\), \(y=g(x)\) と 2直線 \(x=a\),\(x=b\) (\(a<b\)) で囲まれた図形を\(x\)軸まわりに1回転してできる体積\(V\)は、外側の回転体から内側の回転体をくり抜けばよいので
(断面を \(S(x)=π\{f(x)\}^2-π\{g(x)\}^2\) としてもよい)

\(V=π\displaystyle\int_{a}^{b}\{f(x)\}^2dx-π\displaystyle\int_{a}^{b}\{g(x)\}^2dx\)

\(=π\displaystyle\int_{a}^{b}[\{f(x)\}^2-\{g(x)\}^2]dx\)・・・(注2)

(注1)
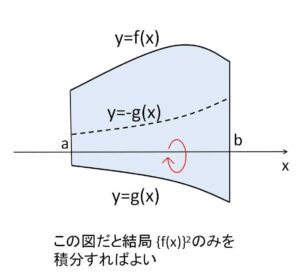
\(f(x),g(x)\)が異符号の場合は、2曲線で囲まれた図形が\(x\)軸の上側にも下側にも存在することになります。このケースでは回転させると重複する部分がでてくるので単純に2乗の差で求めることができません。この場合体積を求めるのに手っ取り早い方法は、一方を折り返す方法です。

(注2)
\(V=π\displaystyle\int_{a}^{b}\{f(x)-g(x)\}^2\)・・・(※)
は誤りです。差の2乗ではなく、必ず2乗の差をとってください。(※)は2関数の差 \(F(x)=f(x)-g(x)\) の\(x\)軸まわりの回転体の体積を意味しているので別物です。式でも
\(\{f(x)-g(x)\}^2=\{f(x)\}^2-2f(x)g(x)+\{g(x)\}^2\)
より違うことが分かります。

(例題)
(1)曲線 \(y=\tan x\) (\(0≦x≦\displaystyle\frac{π}{4}\))、直線 \(x=\displaystyle\frac{π}{4}\)、および\(x\)軸で囲まれる部分を、\(x\)軸まわりに1回転してできる立体の体積を求めよ。

(2)2つの曲線 \(y=\log x\)、\(y=3\log x\) と2つの直線 \(x=e\)、\(x=e^2\) で囲まれた部分を、\(x\)軸の周りに回転させてできる立体の体積を求めよ。

(解答)
(1)

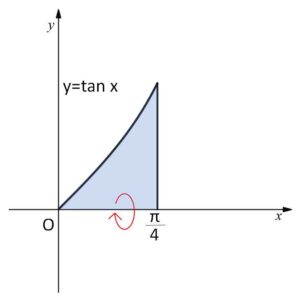
求める体積\(V\)は
\(V=π\displaystyle\int_{0}^{\frac{π}{4}}\tan^2x dx\)

\(=π\displaystyle\int_{0}^{\frac{π}{4}}(\displaystyle\frac{1}{\cos^2x}-1)dx\)

\(=π[\tan x-x]_{0}^{\frac{π}{4}}\)

\(=π-\displaystyle\frac{π^2}{4}\)

(2)

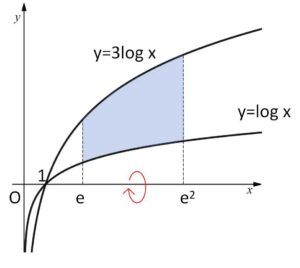
\(3\log x-\log x=2\log x\) より
\(x>1\) のとき \(3\log x>\log x\) だから、求める体積\(V\)は

\(V=π\displaystyle\int_{e}^{e^2}\{(3\log x)-(\log x)^2\}dx\)

\(=8π\displaystyle\int_{e}^{e^2}(\log x)^2dx\)

(\(\log x\)の積分なので部分積分。\(\log x\)が消えるまで2回部分積分する)

\(=8π[x(\log x)^2]_{e}^{e^2}-8π\displaystyle\int_{e}^{e^2}x\cdot2(\log x)\cdot\displaystyle\frac{1}{x}dx\)

\(=8π(4e^2-e)-16π\displaystyle\int_{e}^{e^2}\log xdx\)

\(=8π(4e^2-e)-16π[x\log x]_{e}^{e^2}+16π\displaystyle\int_{e}^{e^2}1dx\)

\(=8π(4e^2-e)-16π(2e^2-e)+16π(e^2-e)\)

\(=16πe^2-8πe\)

\(=8πe(2e-1)\)

以上になります。お疲れ様でした。
ここまで見て頂きありがとうございました。
next→y軸方向の回転　back→断面積と体積