\(y\)軸方向の回転体についてです。
・\(y\)軸方向の回転体の体積
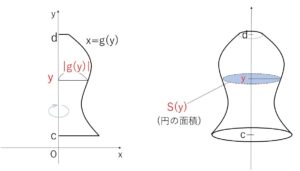
\(y\)軸を\(x\)軸のように見ることで、\(y\)軸まわりに回転させてできた立体の体積も同様の積分で求めることできます。
曲線 \(x=g(y)\) と \(y\)軸、2直線 \(y=c\)、\(y=d\) (\(c<d\)) で囲まれた図形を\(y\)軸まわりに1回転してできる立体の体積\(V\)は次の定積分で表されます。
\(V=π\displaystyle\int_{c}^{d}\{g(y)\}^2dy=π\displaystyle\int_{c}^{d}x^2dy\)
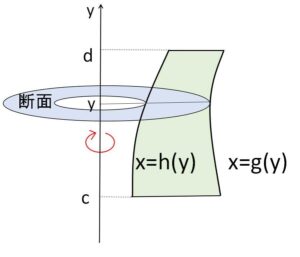
2曲線で囲まれる図形の回転体も同様です。
\(g(y),h(y)\) を同符号、\(|g(y)|≧|h(y)|\) とすると
2曲線 \(x=g(y)\)、\(x=h(y)\) と 2直線 \(y=c\)、\(y=d\) (\(c<d\)) で囲まれた図形を\(y\)軸周りに1回転してできる立体の体積\(V\)は
\(V=π\displaystyle\int_{c}^{d}[\{g(y)\}^2-\{h(y)\}^2]dy\)
ここで、\(x=(yの式)\) で曲線の方程式が与えられる場合は上記のようにそのまま積分をすればよいですが、\(y=f(x)\) の形で曲線の方程式が与えられる場合には
(i)\(x=g(y)\) の形に変形する。(可能ならば)
(ii)置換積分を利用する。
の方法が考えられます。 \(x=g(y)\) と\(x\)軸の間の図形を\(x\)軸周りに1回転させるなどの場合も同様の議論になります。
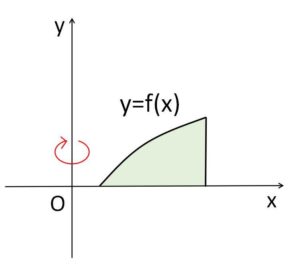
なお、\(y=f(x)\) と \(x\)軸の間の図形を\(y\)軸方向に回転させる場合には(下図)、上記(i)(ii)に加えて、バウムクーヘン分割による方法でも体積を求めることができます。
(例題)
次の曲線や直線で囲まれた図形を\(y\)軸のまわりに1回転してできる立体の体積を求めよ。
(1)\(x=e^y\)、\(y=1\)、\(x\)軸、\(y\)軸
(2)\(y=x^2\)、\(y=\sqrt{x}\)
(3)\(y=\log(x+1)\)、\(y=1\)、\(y\)軸
(4)\(y=\sin x\) (\(0≦x≦\displaystyle\frac{π}{2}\))、\(y=1\)、\(y\)軸
(解答)
以下体積を\(V\)とする。
(1)
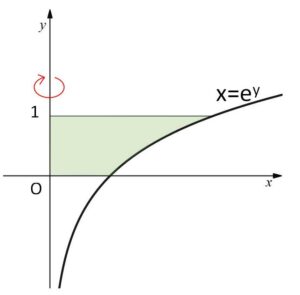
\(V=π\displaystyle\int_{0}^{1}(e^y)^2dy\)
\(=π\left[\displaystyle\frac{e^{2y}}{2}\right]_{0}^{1}\)
\(=\displaystyle\frac{(e^2-1)}{2}π\)
(2)
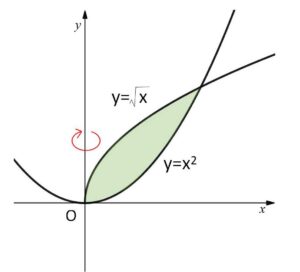
\(x^2=\sqrt{x}\) を解くと
\(\sqrt{x}(x^{\frac{3}{2}}-1)=0\)
よって交点は原点と、点\((1,1)\)
\(y=\sqrt{x}\) より \(x^2=y^4\) だから
\(V=π\displaystyle\int_{0}^{1}(y-y^4)dy\)
\(=π\left[\displaystyle\frac{1}{2}y-\displaystyle\frac{1}{5}y^5\right]_{0}^{1}\)
\(=\displaystyle\frac{3}{10}π\)
(3)
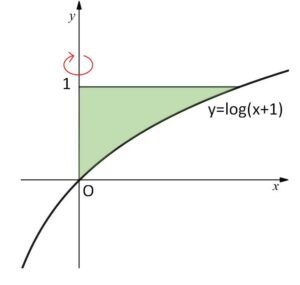
\(y=\log(1+x)\) より \(e^{y}=1+x\)
よって 曲線の方程式は \(x=e^{y}-1\) となるから
\(V=π\displaystyle\int_{0}^{1}(e^y-1)^2dy\)
\(=π\displaystyle\int_{0}^{1}(e^{2y}-2e^y+1)dy\)
\(=π\left[\displaystyle\frac{e^{2y}}{2}-2e^y+y\right]_{0}^{1}\)
\(=π(\displaystyle\frac{e^2}{2}-2e+1-\displaystyle\frac{1}{2}+2)\)
\(=π(\displaystyle\frac{e^2}{2}-2e+\displaystyle\frac{5}{2})\)
(4)
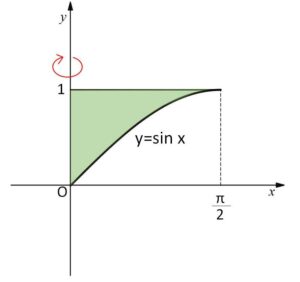
(置換積分します)
\(y=\sin x\) より \(dy=\cos x dx\) だから
\(V=π\displaystyle\int_{0}^{1}x^2dy\)
\(=π\displaystyle\int_{0}^{\frac{π}{2}}x^2\cos xdx\) (\(x\)の積分に変換した。積分区間の対応に注意)
(2回部分積分をして)
\(=π[x^2\sin x]_{0}^{\frac{π}{2}}-π\displaystyle\int_{0}^{\frac{π}{2}}2x\sin xdx\)
\(=\displaystyle\frac{π^3}{4}-π[2x(-\cos x)]_{0}^{\frac{π}{2}}-π\displaystyle\int_{0}^{\frac{π}{2}}2\cos xdx\)
\(=\displaystyle\frac{π^3}{4}+0-π[2\sin x]_{0}^{\frac{π}{2}}\)
\(=\displaystyle\frac{π^3}{4}-2π\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→陰関数と回転体 back→回転体の体積