陰関数で表された曲線で囲む図形の回転体です。
グラフの概形については対称性があるかまず確認します。
(例題1)
\(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\) (\(a,b\)は正の数)
で囲まれた図形を\(x\)軸まわりに回転してできる立体の体積を求めよ。
(解答)
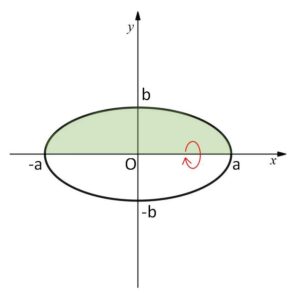
\(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\) より
\(y^2=b^2(1-\displaystyle\frac{x^2}{a^2})\)
よって体積\(V\)は
\(V=π\displaystyle\int_{-a}^{a}b^2(1-\displaystyle\frac{x^2}{a^2})dx\)
(偶関数の定積分。結局第1象限の部分だけを考えればよいことになる)
\(=2π\displaystyle\int_{0}^{a}b^2(1-\displaystyle\frac{x^2}{a^2})dx\)
\(=2πb^2\left[x-\displaystyle\frac{x^3}{3a^2}\right]_{0}^{a}\)
\(=\displaystyle\frac{4}{3}πab^2\)
(例題2)
\(x^4+y^2=x^2\) で表される曲線を\(C\)とする。
(1)\(C\)のグラフの概形をかけ。
(2)\(C\)で囲まれる図形を\(x\)軸周りに回転させてできる立体の体積を求めよ。
(3)\(C\)で囲まれる図形を\(y\)軸周りに回転させてできる立体の体積を求めよ。
(解答)
(1)
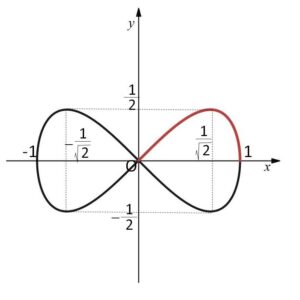
よって、\(x,y≧0\) について調べれば十分です。\(y=\cdots\) の形に簡単に変形できるので、これを微分します。
\(x^4+y^2=x^2\)・・・①
点\((a,b)\) が①のグラフ上にあるとすると、\(a^4+b^2=a^2\)・・・②
すると\((-a,b)\)、\((a,-b)\)を①に代入すると②を満たすので、①のグラフは\(x,y\)軸について対称になる。
よって、\(x,y≧0\) について考えてグラフを折り返せばよい。
①より
\(y=\sqrt{x^2-x^4}\) であり、定義域は \(x^2(1-x^2)≧0\) より
\(0≦x≦1\)
\(f(x)=x^2-x^4\) とおくと
\(f'(x)=2x-4x^3=2x(1-2x^2)\) より
\(0≦x≦\displaystyle\frac{1}{\sqrt{2}}\) で単調増加
\(\displaystyle\frac{1}{\sqrt{2}}≦x≦1\) で単調減少
極大値は \(f(\displaystyle\frac{1}{\sqrt{2}})=\displaystyle\frac{1}{4}\)
以上からグラフの概形は次のようになる。
(2)
\(x^4+y^2=x^2\)・・・① より
\(y^2=x^2-x^4\)
グラフは\(x,y\)軸について対称なので求める体積\(V\)は
\(V=2\displaystyle\int_{0}^{1}πy^2dx\)
\(=2π\displaystyle\int_{0}^{1}(x^2-x^4)dx\)
\(=2π\left[\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{5}x^5\right]_{0}^{1}\)
\(=\displaystyle\frac{4}{15}π\)
(3)
\(x^4+y^2=x^2\) を \(x^2\)の2次方程式とみると
\((x^2)^2-x^2+y^2=0\) より
\(x^2=\displaystyle\frac{1±\sqrt{1-4y^2}}{2}\)・・・②
です。グラフは\(x,y\)軸対称なので、\(x,y≧0\) の部分を考えればよく、あとは上側と下側の関数が②の\(±\)のどちらになっているか(\(+\)がそのまま上側)を判断するだけです。(詳しくは参考参照)
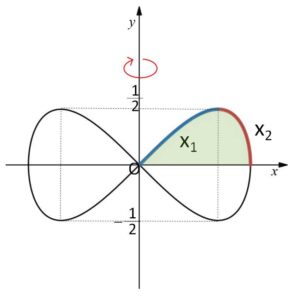
\(x^4+y^2=x^2\)・・・① より
\(x^4-x^2+y^2=0\)
\(x^2\)の2次方程式とみると、解の公式より
\(x^2=\displaystyle\frac{1±\sqrt{1-4y^2}}{2}\)・・・②
グラフは\(x,y\)軸について対称だから、\(x,y≧0\)の場合を考えて2倍すればよく、図の\(x_1,x_2\)の2乗はそれぞれ②の\(-,+\)に対応するから、体積\(V\)は
\(V=2\displaystyle\int_{0}^{\frac{1}{2}}π(x_2^2-x_1^2)dy\)
\(=2π\displaystyle\int_{0}^{\frac{1}{2}}(\displaystyle\frac{1+\sqrt{1-4y^2}}{2}-\displaystyle\frac{1-\sqrt{1-4y^2}}{2})dy\)
\(=2π\displaystyle\int_{0}^{\frac{1}{2}}\sqrt{1-4y^2}dy\)
(円の面積に帰着させる。三角関数で置換してもよい)
\(=2π\cdot2\displaystyle\int_{0}^{\frac{1}{2}}\sqrt{\displaystyle\frac{1}{4}-y^2}dy\)
(半径\(\frac{1}{2}\)の四分円)
\(=4π\cdot\displaystyle\frac{1}{4}\cdot(\displaystyle\frac{1}{2})^2π\)
\(=\displaystyle\frac{π^2}{4}\)
(参考)
\(x^4+y^2=x^2\)・・・①
(3)より
\(x^2=\displaystyle\frac{1+\sqrt{1-4y^2}}{2}\)・・・(i)
\(x^2=\displaystyle\frac{1-\sqrt{1-4y^2}}{2}\)・・・(ii)
でしたが、どちらも平方根をとり \(x=\cdots\) の形にすると
\(x=\sqrt{\displaystyle\frac{1+\sqrt{1-4y^2}}{2}}\)・・・(i-a)
\(x=-\sqrt{\displaystyle\frac{1+\sqrt{1-4y^2}}{2}}\)・・・(i-b)
\(x=\sqrt{\displaystyle\frac{1-\sqrt{1-4y^2}}{2}}\)・・・(ii-a)
\(x=-\sqrt{\displaystyle\frac{1-\sqrt{1-4y^2}}{2}}\)・・・(ii-b)
となるので、曲線①は\(y\)の関数で表すと全部で4種類になります。
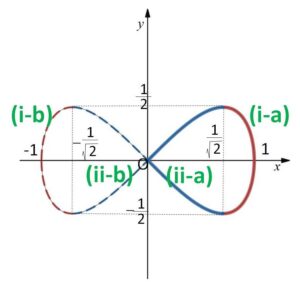
なお、\(x\)の関数とみると
\(y=±\sqrt{x^2-x^4}\)
なので、全部で2種類です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→重複部分と回転体 back→y軸方向の回転体