x,y軸に平行な直線に関する回転体

\(x,y\)軸に平行な直線に関する回転体の体積を求める例題です。

(例題1)
\(y=\sin x\) (\(0≦x≦π\)) と\(x\)軸とで囲まれた図形を\(D\)とする。\(D\)を 直線 \(y=-1\) の周りに回転させてできる立体の体積を求めよ。

(解答)

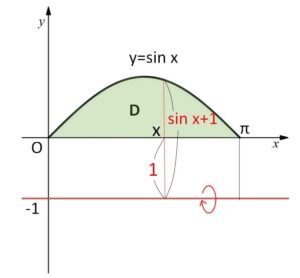
\(x\)座標が\(x\)であるときの断面積\(S(x)\)は
\(S(x)=π\{\sin x-(-1)\}^2-π\cdot1^2\)
\(=π(\sin x+1)^2-π\)
\(=π(\sin^2x+2\sin x)\) だから、体積\(V\)は

\(V=\displaystyle\int_{0}^{π}π(\sin^2x+2\sin x)dx\)
\(=π\displaystyle\int_{0}^{π}\left(\displaystyle\frac{1-\cos2x}{2}+2\sin x\right)dx\)
\(=π\left[\displaystyle\frac{1}{2}x-\displaystyle\frac{\sin 2x}{4}-2\cos x\right]_{0}^{π}\)
\(=π\left(\displaystyle\frac{π}{2}+2+2\right)\)

\(=\displaystyle\frac{π}{2}(π+8)\)

(別解1)
内側の立体を円柱とみて、この円柱のくり抜きを考えてもよい。
\(V=π\displaystyle\int_{0}^{π}(\sin x+1)^2dx-1^2π\cdotπ\)

(別解2)

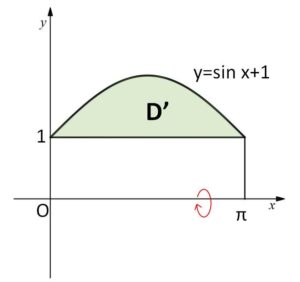
回転軸 \(y=-1\) が\(x\)軸に重なるように全体を\(y\)軸の方向に\(+1\)平行移動する。
\(y=\sin x+1\) と \(y=1\) (\(x\)軸の平行移動後の直線) で囲まれた図形を\(x\)軸まわりに1回転させてできる立体の体積\(V\)が求めるものだから
\(V=π\displaystyle\int_{0}^{π}(\sin x+1)^2dx-π\displaystyle\int_{0}^{π}1^2dx\)

(例題2)
楕円 \(\displaystyle\frac{x^2}{4}+y^2=1\) で囲まれた図形を直線 \(x=4\) のまわりに1回転させてできる立体の体積\(V\)を求めよ。

(解答)

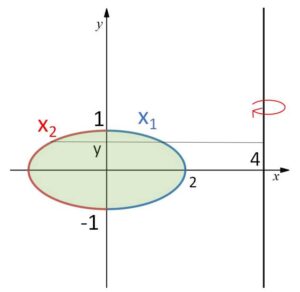
\(\displaystyle\frac{x^2}{4}+y^2=1\) より
\(x^2=4(1-y^2)\)
\(x=±2\sqrt{1-y^2}\)

\(x_1=2\sqrt{1-y^2}\)、\(x_2=-2\sqrt{1-y^2}\) とおくと
回転体の\(y\)座標が\(y\)のときの断面積\(S(y)\)は

\(S(y)=π(4-x_2)^2-π(4-x_1)^2\)
\(=π(4+2\sqrt{1-y^2})^2-π(4-2\sqrt{1-y^2})^2\)
\(=32π\sqrt{1-y^2}\)

よって体積\(V\)は
\(V=\displaystyle\int_{-1}^{1}32π\sqrt{1-y^2}dy\)

(半径\(1\)の半円の面積)

\(=32π×\displaystyle\frac{1}{2}\cdot1^2π\)

\(=16π^2\)

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→斜軸の回転体　back→極座標と回転体