指数方程式の解の個数に関する問題について見ていきます。
(例題1)
\(x\)の方程式 \(4^x-a\cdot2^{x+1}+a^2-4=0\)
が正の解と負の解を1つずつもつように\(a\)の値の範囲を定めよ。
\(t^2-2at+a^2-4=0\)・・・(1) です。
条件は、\(x\)が正の解と負の解をもつときなので、\(t\)としてはどうなるかというと、\(y=2^x\) のグラフを考えると、
①\(x>0\)のとき \(t>1\)
②\(x<0\)のとき \(0<t<1\)
だから、2次方程式(1)が \(t>1\) と \(0<t<1\) の範囲にそれぞれ1つずつ解をもてばよいことになります。
(解答)
\(4^x-a\cdot2^{x+1}+a^2-4=0\) より
\(2^{2x}-2a\cdot2^{x}+a^2-4=0\)
\(2^{x}=t\) (\(t>0\)) とおくと
\(t^2-2at+a^2-4=0\)・・・(1)
①\(x<0\) のとき \(0<t<1\)
②\(x>0\) のとき \(t>1\)
だから、方程式(1)が \(0<t<1\) と \(t>1\) の範囲に1つずつ解をもてばよい。
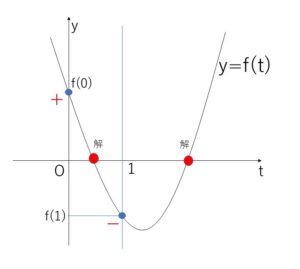
\(f(t)=t^2-2at+a^2-4\) とおくと、図より
\(f(0)>0\) かつ \(f(1)<0\)
また、\(0<t<1\) に重解でないただ1つの解をもつ場合は、他に \(f(0)<0\) かつ \(f(1)>0\) のときがありますが、これは\(t>1\)に解をもたないので不適です。
\(f(0)=a^2-4>0\)・・・(2)
\(f(1)=1-2a+a^2-4<0\)・・・(3)
それぞれ\(a\)について解くと
(2)\(a<-2\) または \(a>2\)
(3)\(-1<a<3\)
(2)かつ(3)より
\(2<a<3\)
(例題2)
\(a\)を定数とする。
\(2^{2x}-(a+1)2^x+(a^2-\displaystyle\frac{7}{4})=0\)・・・①
について
(1)①を満たす相違なる\(x\)の実数値が2個存在するための\(a\)の条件を求めよ。
(2)①を満たす\(x\)の実数値がただ1個だけ存在するための\(a\)の条件を求めよ。
(解答)
\(2^x=t(>0)\) とおくと
\(2^{2x}-(a+1)2^x+(a^2-\displaystyle\frac{7}{4})=0\)・・・① より
\(t^2-(a+1)t+(a^2-\displaystyle\frac{7}{4})=0\)・・・②
(1)
\(x\)の方程式①が異なる2つの実数解をもつとき、\(t\)の方程式②は異なる2つの正の実数解をもつ。
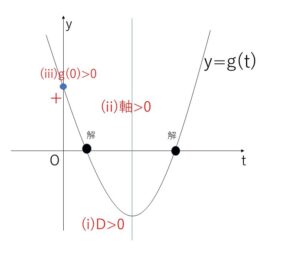
\(g(t)=t^2-(a+1)t+(a^2-\displaystyle\frac{7}{4})\)
とおくと、
(i)判別式 \(D>0\)
(ii)軸 \(\displaystyle\frac{a+1}{2}>0\)
(iii)端点 \(g(0)>0\)
(i)より
\((a+1)^2-4(a^2-\displaystyle\frac{7}{4})>0\)
これを解くと、\(-\displaystyle\frac{4}{3}<a<2\)
(ii)より
\(a>-1\)
(iii)より
\(a^2-\displaystyle\frac{7}{4}>0\)
よって \(a<-\displaystyle\frac{\sqrt{7}}{2}\) または \(a>\displaystyle\frac{\sqrt{7}}{2}\)
(i)かつ(ii)かつ(iii)より
\(\displaystyle\frac{\sqrt{7}}{2}<a<2\)
(i)\(-\displaystyle\frac{4}{3}<a<2\) (ii)\(a>-1\) (iii) \(a>\displaystyle\frac{\sqrt{7}}{2}\)
の共通部分が答えです。
(2)
\(g(t)=t^2-(a+1)t+(a^2-\displaystyle\frac{7}{4})=0\)・・・②
において、
(ア)②の解の1つが正、もう1つは0以下 (イ)②が正の重解をもつ
の2パターンになりますが、(ア)をさらに
(ア1)1つが負、1つが正 (ア2)1つが0、1つが正
に分けます。
このイコールつきの不等式で、
\(g(0)<0\)のほうは、1つが負、1つが正となって適するのですが、
\(g(0)=0\)は、1つが0であるだけでもう1つは正でも負でもよい条件になってしまいます。
\(g(t)=t^2-(a+1)t+(a^2-\displaystyle\frac{7}{4})=0\)・・・②
において、ただ1つの正の解\(t\)をもてばよい。
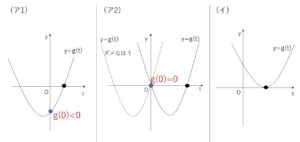
(ア1)正、負の解を1つずつもつとき
\(g(0)=a^2-\displaystyle\frac{7}{4}<0\)
これを解いて \(-\displaystyle\frac{\sqrt{7}}{2}<a<\displaystyle\frac{\sqrt{7}}{2}\)
(ア2)正の解と解\(t=0\)をもつとき
②に\(t=0\) を代入して
\(a^2-\displaystyle\frac{7}{4}=0\)
\(a=±\displaystyle\frac{\sqrt{7}}{2}\)
\(a=\displaystyle\frac{\sqrt{7}}{2}\) を②に代入して
\(t^2-(\displaystyle\frac{\sqrt{7}}{2}+1)t=0\)
\(t\{t-(\displaystyle\frac{\sqrt{7}}{2}+1)\}=0\)
もう1つの解は正となり適する。
\(a=-\displaystyle\frac{\sqrt{7}}{2}\) も同様に考えると
もう1つの解は、\(t=-\displaystyle\frac{\sqrt{7}}{2}+1\)
で負の数なので不適。
よって、\(a=\displaystyle\frac{\sqrt{7}}{2}\)
(イ)正の重解をもつとき
\(D=(a+1)^2-4(a^2-\displaystyle\frac{7}{4})=0\)
これを解くと、\(a=2,-\displaystyle\frac{4}{3}\)
重解は
\(x=\displaystyle\frac{a+1}{2}\) なので、
\(a=-\displaystyle\frac{4}{3}\) のときは、負の重解となり不適。
よって、\(a=2\)
以上より
\(-\displaystyle\frac{\sqrt{7}}{2}<a≦\displaystyle\frac{\sqrt{7}}{2}\), \(a=2\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→指数方程式と有理数解 back→指数関数の最大最小