対数方程式の解に関する問題について見ていきます。
(例題1)
\((\log_{2}x)^2-(a+1)\log_{2}x+(a^2-\displaystyle\frac{7}{4})=0\)
を満たす相異なる\(x\)の実数値が2個存在するように、定数\(a\)の範囲を求めよ。
(解答)
\(\log_{2}x=t\) とおくと、\(t\)は実数全体をとる。
与式は
\(t^2-(a+1)t+(a^2-\displaystyle\frac{7}{4})=0\)・・・①
\(t\)の方程式①が異なる2つの実数解を持てば、異なる実数値\(x\)が2個存在することになるので
\(D=(a+1)^2-4(a^2-\displaystyle\frac{7}{4})>0\)
\(3a^2-2a-8<0\)
\((3a+4)(a-2)<0\)
したがって
\(-\displaystyle\frac{4}{3}<a<2\)
(例題2)
(1)\(x\)の関数 \(t=\log_{2}(x^2+\sqrt{2})\) の最小値とそのときの\(x\)を求めよ。
(2)\(a\)を定数とするとき、\(x\)の方程式
\(\{\log_{2}(x^2+\sqrt{2})\}^2-2\log_{2}(x^2+\sqrt{2})+a=0\)・・・・①
が解をもつ条件は \(a≦(ア)\) である。\(a=(ア)\) のとき方程式①は \((イ)\) 個の解をもち、また方程式①が3個の解をもつのは \(a=(ウ)\) のときである。
(解答)
(1)
底が\(2\)なので、真数が最小値のときを考えて
\(t=\log_{2}(x^2+\sqrt{2})≧\log_{2}(0^2+\sqrt{2})=\displaystyle\frac{1}{2}\)
よって \(x=0\) のとき 最小値 \(\displaystyle\frac{1}{2}\)
(2)
方程式①は
\(t^2-2t+a=0\)・・・② (ただし \(t≧\displaystyle\frac{1}{2}\))
②の左辺をそのまま考えても解けますが、定数\(a\)が簡単に分離できるので定数分離します。
②が \(t≧\displaystyle\frac{1}{2}\) の範囲で解をもてば、方程式①は解\(x\)をもつことになる。
②より
\(-t^2+2t=a\)
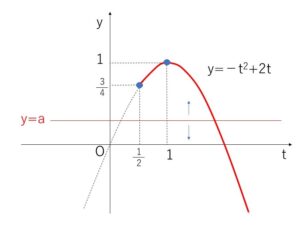
\(y=-t^2+2t=-(t-1)^2+1\)
\(y=a\) のグラフを考えて
\(a≦1\)・・・(ア)
次に \(a=1\) のとき方程式②は \(t=1\) が解
\(t=\log_{2}(x^2+\sqrt{2})=1\) より
\(x^2+\sqrt{2}=2\)
\(x^2=2-\sqrt{2}\)
\(x=±\sqrt{2-\sqrt{2}}\)
よって 2個・・・(イ)
(イ)で具体的に\(t=1\)のときをやりましたが、\(t=\log_{2}(x^2+\sqrt{2})\) で\(x\)のほうも2次式となっているので、\(t\)1個につき、\(x\)が2個対応しています。先ほどのグラフから\(t\)としての解は1個か2個なので、\(x\)としては2個か4個が原則です。
では\(x\)が3個になるのはどういう場合かというと、\(t\)が1個のときはMaxで\(x\)2個なので不適。よって \(t\)は2個となるわけですが、2個の\(t\)のうち一方は\(x\)としての解が2個で、もう一方が\(x\)としての解は1個(\(x\)の重解になっている)ときに合計3個になります。重解になっているのは \(x=0\) とすぐにわかるので\(a\)もすぐに求まります。
方程式①が3解をもつときは、
\(t^2-2t+a=0\)・・・②
が異なる2つの解\(t\)をもつときで、その2解を\(t_1,t_2\) とおくと
\(t_1=\log_{2}(x^2+\sqrt{2})\)
が2つの異なる実数解\(x\)をもち
\(t_2=\log_{2}(x^2+\sqrt{2})\)
が重解\(x\)をもつときである。
重解は \(x=0\) で、このとき \(t_2=\displaystyle\frac{1}{2}\)
\(t=\displaystyle\frac{1}{2}\)が②の解となるときは
グラフより \(a=\displaystyle\frac{3}{4}\)・・・(ウ)
(このとき もう一方の解\(t_1\) について解\(x\)は2個となる)
(例題3)
\(a\)を実数とするとき、\(x\)に関する方程式
\(\log_{3}(x-1)=\log_{9}(4x-a-3)\)
が異なる2つの実数解をもつとき、\(a\)のとりうる値の範囲を求めよ。
真数条件より
\(x-1>0\) かつ \(4x-a-3>0\)
つまり
\(x>1\) かつ \(x>\displaystyle\frac{a+3}{4}\)・・・①
\(\log_{3}(x-1)=\log_{9}(4x-a-3)\) より
\(\log_{3}(x-1)=\displaystyle\frac{\log_{3}(4x-a-3)}{2}\)
\(\log_{3}(x-1)^2=\log_{3}(4x-a-3)\)
よって
\((x-1)^2=4x-a-3\)・・・(※)
整理して
\(x^2-6x+a+4=0\)・・・②
①の2つの範囲の共通部分は、\(a\)によって異なるので場合分けします。\(\displaystyle\frac{a+3}{4}=1\) が境目です。
(i) \(\displaystyle\frac{a+3}{4}≦1\) つまり \(a≦1\) のとき
①の2つの範囲の共通部分は \(x>1\)
したがって
②が\(x>1\)で2つの実数解を持てばよいことになる。
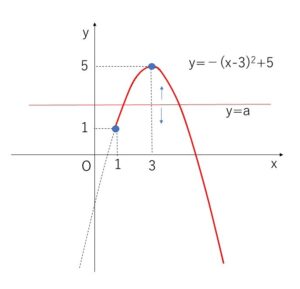
\(-x^2+6x-4=a\)
\(-(x-3)^2+5=a\)
\(y=-(x-3)^2+5\) と \(y=a\) のグラフが2つの共有点をもつとき
\(1<a<5\)
\(a≦1\) を満たさないので不適。
(ii)\(\displaystyle\frac{a+3}{4}>1\) つまり \(a>1\) のとき
①の2つの範囲の共通部分は \(x>\displaystyle\frac{a+3}{4}\)
したがって
②が\(x>\displaystyle\frac{a+3}{4}\)で2つの実数解を持てばよいことになる。
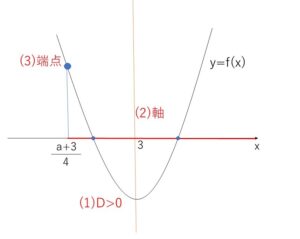
\(f(x)=x^2-6x+a+4\) とおくと条件は
(1)判別式 \(\displaystyle\frac{D}{4}=9-(a+4)>0\)
(2)軸 \(3>\displaystyle\frac{a+3}{4}\)
(3)端点 \(f(\displaystyle\frac{a+3}{4})>0\)
(1)より \(a<5\)
(2)より \(a<9\)
(3)より
\((\displaystyle\frac{a+3}{4})^2-6(\displaystyle\frac{a+3}{4})+a+4>0\)
整理して
\(a^2-2a+1>0\)
\((a-1)^2>0\)
\(a≠1\)
\(a>1\) とあわせて
\(1<a<5\)
(※)の式に着目すると、実はもっと楽な解法もあります。
一旦問題の解く方針を整理すると
\(x>1\) かつ \(x>\displaystyle\frac{a+3}{4}\)・・・①
の範囲で
\(x^2-6x+a+4=0\)・・・②
が2つの実数解をもてばよいということです。
②式を導く途中の式で
\((x-1)^2=4x-a-3\)・・・(※)
という式がありましたが、\(x>1\) (\(x\)は実数) のとき、(※)の右辺は正の数になります。
ということは、\(4x-a-3>0\) であり、これは①の2番目の \(x>\displaystyle\frac{a+3}{4}\) と同じ式です。そうすると、結局①の \(x>1\) を満たすだけでよいことになるので、
\(x^2-6x+a+4=0\)・・・②
が \(x>1\) で2つの異なる実数解をもてばよいことになります。
あとは定数分離すれば簡単に\(a\)の範囲が求まります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→対数関数と領域 back→対数関数の最大最小②