集合の要素に未知数が含まれる場合、条件より未知数を決定する問題を見ていきます。
(問題1)
2つの集合を、 \(A=\{x|-2≦x≦3\}\), \(B=\{x|k-6≦x≦k\}\) (\(k\)は定数) とするとき、\(A \subset B\) となる\(k\)の値の範囲を求めよ。
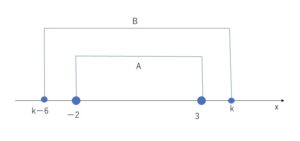
数直線で考えてみます。
(解答)
図より、\(A \subset B\)となるのは、
\(k-6≦-2\) かつ \(k≧3\)
よって \(3≦k≦4\)
境目である \(k-6=-2\) と \(k=3\) の場合でも、\(A \subset B\)となるので、答えの不等号には=がつきます。
(問題2)
次のような集合\(A,B,C\)がある。ただし、\(a,b,c\)は整数である。
\(A=\{2,4,2c-1\}\), \(B=\{3,2c-a-1\}\), \(C=\{2,2c+b-2\}\)
次のような集合\(A,B,C\)がある。ただし、\(a,b,c\)は整数である。
\(A=\{2,4,2c-1\}\), \(B=\{3,2c-a-1\}\), \(C=\{2,2c+b-2\}\)
(1)\(A \cup B=\{2,3,4\}\) となるような、\(a,c\)の値を求めよ。
(2)\(B=C \subset A\) となるような \(a,b\)の値を求めよ。
(2)\(B=C \subset A\) となるような \(a,b\)の値を求めよ。
(解答)
(1)
(1)
\(A \cup B=\{2,3,4\}\) より \(A\)の要素 \(2c-1\)は\(3\)です。また、\(B\)の要素\(2c-a-1\)は、\(2\)か\(4\)になります。(\(3\)だと集合\(B\)の要素に同じ数が含まれるので不適とします)
\(2c-1=3\) かつ \(2c-a-1=2\) または \(4\) だから
\((a,c)=(1,2),(-1,2)\)
\((a,c)=(1,2),(-1,2)\)
(2)
\(B=C\) より、\(B=C=\{2,3\}\)となります。また、\(B=C \subset A\)だから、\(A\)の要素に\(2,3\)があることになりますが、\(2\)は既にあるので、\(2c-1=3\)となります。
\(B=C\) より、\(B=C=\{2,3\}\)であるから、
\(2c-a-1=2\), \(2c+b-2=3\)・・・①
\(2c-a-1=2\), \(2c+b-2=3\)・・・①
また、\(B=C \subset A\) より \(A\)の要素に\(3\)があることになるので
\(2c-1=3\)・・・②
\(2c-1=3\)・・・②
①②を解いて、\(c=2\), \(a=1\), \(b=1\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
ここまで見て頂きありがとうございました。