要素の個数の最大最小値問題は、ベン図を利用します。
(問題)
50人のクラスで、兄弟のいる人は33人、姉妹のいる人は27人であった。このとき、ひとりっ子は (ア) 人以下である。兄弟、姉妹ともにいる人は (イ) 人以上いる。また、兄弟だけいる人は、少なくとも (ウ) 人、多くて (エ) 人までであり、姉妹だけいる人は多くても (オ) 人までである。
まず、全体集合\(U\)とその部分集合\(A,B\)について各領域の集合も考えるとベン図は次の通りです。
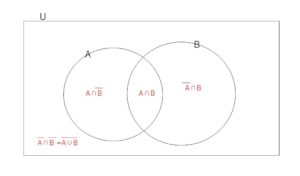
\(n(A \cup B)\)が最大となるときのベン図を考えます。
\(n(A \cup B)\)\(=n(A)+n(B)-n(A \cap B)\) なので、
\(n(A \cap B)\) が最小となるとき、最大値をとります。このときベン図は、次のようになります。
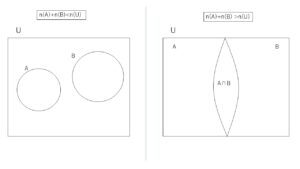
\(n(A \cup B)\)が最小となるときのベン図は次の通りです。
このとき、\(n(A \cap B)\) が最大となり、片方がすっぽりともう片方に入る形になります。
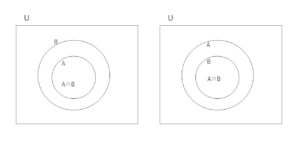
(解答)
兄弟がいる人の集合を\(A\)、姉妹がいる人の集合を\(B\)とする。
(ア)
求める値は、\(n(\overline A \cap \overline B)\)の最大値であり、
\(n(\overline A \cap \overline B)\)\(=n(U)-n(A \cup B)\) だから
\(n(A \cup B)\)が最小値となるときを考えればよい。ベン図は次の通り。
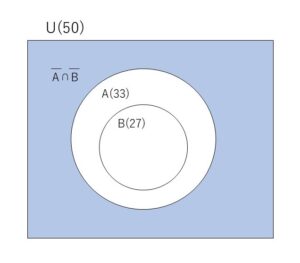
このとき、\(n(A \cup B)=n(A)=33\) だから
求める最大値は \(50-33=\)\(17\)
(イ)
求める値は、\(n(A \cap B)\)の最小値。ベン図は次の通り。
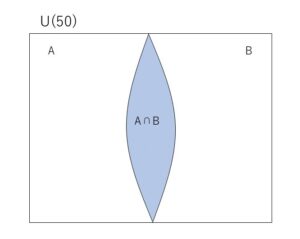
このとき、\(n(A \cup B)\)\(=n(U)=50\) だから
\(n(A \cup B)\)\(=n(A)+n(B)-n(A \cap B)\) より
\(50=33+27-n(A \cap B)\) となり
\(n(A \cap B)=\)\(10\)
(ウ)
求める値は、\(n(A \cap \overline B)\) の最小値
\(n(A \cap \overline B)\)\(=n(A)-n(A \cap B)\) だから、
\(n(A \cap B)\)が最大値をとるときを考えればよい。ベン図は次の通り。
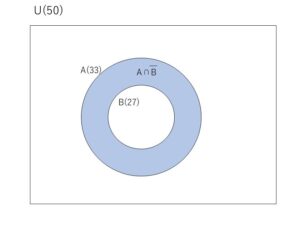
よって、求める値は
\(n(A\cap \overline B)\)\(=n(A)-n(B)\)\(=33-27=\)\(6\)
(エ)
求める値は、\(n(A \cap \overline B)\) の最大値
\(n(A \cap \overline B)\)\(=n(A)-n(A \cap B)\) だから、
\(n(A \cap B)\) が最小となるときを考えればよい。ベン図は次の通り。
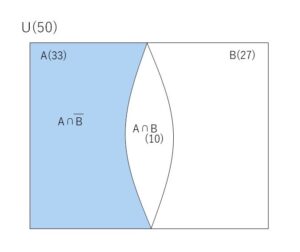
このとき、(イ)より \(n(A \cap B)=\)\(10\) だから
求める値は
\(n(A \cap \overline B)\)\(=n(A)-n(A \cap B)\)\(=33-10=\)\(23\)
(オ)
求める値は、\(n(\overline A \cap B)\) の最大値
\(n(\overline A \cap B)\)\(=n(B)-n(A \cap B)\) だから
\(n(A \cap B)\) が最小となるときを考えればよい。ベン図は次の通り。
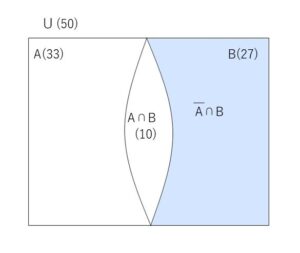
(エ)と同様だから、\(n(A \cap B)=\)\(10\)
求める値は
\(n(\overline A \cap B)\)\(=n(B)-n(A \cap B)\)\(=27-10=\)\(17\)
以上になります。 お疲れさまでした。
ここまで見て頂きありがとうございました。