数列を利用する図形問題について見ていきます。
(例題1)
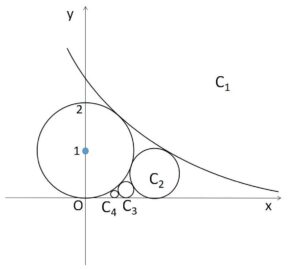
円 \(x^2+(y-1)^2=1\) と外接し、\(x\)軸と接する円で中心の\(x\)座標が正であるものを条件\(P\)を満たす円ということにする。
(1)条件\(P\)を満たす円の中心は、曲線 \(y=(ア)\) (\(x>0\)) の上にある。また、条件\(P\)を満たす半径\(9\)の円を\(C_1\)とし、その中心の\(x\)座標を\(a_1\)とすると、\(a_1=(イ)\) である。
(2)条件\(P\)を満たし円\(C_1\)に外接する円を\(C_2\)とする。また、\(n=3,4,5,\cdots\) に対し、条件\(P\)を満たし、円\(C_{n-1}\)に外接し、かつ円\(C_{n-2}\)と異なる円を\(C_n\)とする。円\(C_n\)の中心の\(x\)座標を\(a_n\)とするとき、自然数\(n\)に対し\(a_{n+1}\)を\(a_n\)を用いて表しなさい。
(2) (1),(2)で定めた数列\(\{a_n\}\)の一般項を求めなさい。
(解答)
(1)

条件\(P\)を満たす円の中心の座標を\((X,Y)\)とすると、図で2円の中心間の距離の2乗から
\(X^2+(Y-1)^2=(1+Y)^2\)
整理して\(X→x\), \(Y→y\) とすると
\(y=\displaystyle\frac{1}{4}x^2\) (\(x>0\))
よって、\(C_1\)の中心の座標は \((a_{1},\displaystyle\frac{1}{4}a_{1}^2)\) とおけるので、半径が\(9\)であることから
\(\displaystyle\frac{1}{4}a_{1}^2=9\)
ゆえに \(a_1=6\)
(2)
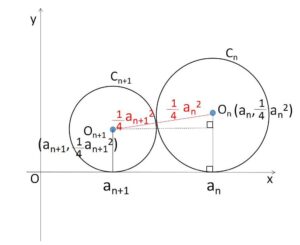
円\(C_n,C_{n+1}\)の中心を\(O_n,O_{n+1}\)とおくと、これらの座標は(1)より
\(O_n(a_n,\displaystyle\frac{1}{4}a_n^2),\ O_{n+1}(a_{n+1},\displaystyle\frac{1}{4}a_{n+1}^2)\)
よって円\(C_n,C_{n+1}\)の半径は、\(\displaystyle\frac{1}{4}a_n^2,\displaystyle\frac{1}{4}a_{n+1}^2\) だから、\(O_nO_{n+1}\)間の距離の2乗より
\((a_{n+1}-a_{n})^2+(\displaystyle\frac{1}{4}a_n^2-\displaystyle\frac{1}{4}a_{n+1}^2)^2=(\displaystyle\frac{1}{4}a_n^2+\displaystyle\frac{1}{4}a_{n+1}^2)^2\)
ゆえに
\((a_{n+1}-a_{n})^2=\displaystyle\frac{1}{4}a_n^2a_{n+1}^2\)
ここで図より数列\(\{a_n\}\)は単調減少数列だから、\(a_{n+1}<a_n\)である。
したがって
\(a_{n}-a_{n+1}=\displaystyle\frac{1}{2}a_na_{n+1}\ (>0)\)
\(a_{n+1}\)について解くと
\(a_{n+1}(\displaystyle\frac{1}{2}a_n+1)=a_n\)
\(a_n=-2\) とすると、\(0=-2\) となり等式を満たさないので、\(a_n≠-2\)だから
\(a_{n+1}=\displaystyle\frac{2a_n}{a_n+2}\)
(3)
(1)(2)より
\(a_1=6\)
\(a_{n+1}=\displaystyle\frac{2a_n}{a_n+2}\)
漸化式と\(a_1\)より帰納的に\(a_n>0\)だから、逆数をとると
\(\displaystyle\frac{1}{a_{n+1}}=\displaystyle\frac{1}{a_n}+\displaystyle\frac{1}{2}\) (等差型)
よって
\(\displaystyle\frac{1}{a_{n}}=\displaystyle\frac{1}{a_1}+(n-1)\cdot\displaystyle\frac{1}{2}\)
\(=\displaystyle\frac{1}{6}+(n-1)\cdot\displaystyle\frac{1}{2}\)
\(=\displaystyle\frac{3n-2}{6}\)
したがって
\(a_n=\displaystyle\frac{6}{3n-2}\)
(例題2)
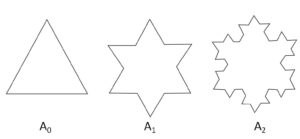
面積\(1\)の正三角形\(A_0\)からはじめて、図のような図形\(A_1,A_2,\cdots\)を作る。ここで、\(A_n\)は、\(A_{n-1}\)の各辺の3等分点を頂点にもつ正三角形を\(A_{n-1}\)の外側につけ加えてできる図形である。
(1)図形\(A_n\)の辺の数\(l_n\)を求めよ。
(2)図形\(A_n\)の周の長さ\(L_n\)を求めよ。
(3)図形\(A_n\)の面積\(S_n\)を求めよ。
(解答)
(1)
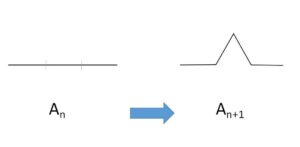
\(A_{n}\)の一辺が、\(A_{n+1}\)では4辺になるから
\(l_{n+1}=4l_n\)
\(l_0=3\) より
\(l_n=3\cdot4^n\)
(\(0\)スタートなので\(n\)乗)
(2)
図形\(A_n\)の一辺の長さを\(a_n\)とおくと
\(a_{n+1}=\displaystyle\frac{1}{3}a_n\)
図形\(A_0\)(正三角形)の面積は\(1\)だから
\(\displaystyle\frac{1}{2}a_0^2\sin60°=1\) より
\(a_0=\displaystyle\frac{2}{\sqrt[4]{3}}\)
よって漸化式から
\(a_n=\displaystyle\frac{2}{\sqrt[4]{3}}(\displaystyle\frac{1}{3})^n\)
したがって周の長さ\(L_n\)は(1)より
\(L_n=a_n×l_n\)
\(=\displaystyle\frac{2}{\sqrt[4]{3}}(\displaystyle\frac{1}{3})^n×3\cdot4^n\)
\(=\displaystyle\frac{6}{\sqrt[4]{3}}(\displaystyle\frac{4}{3})^n\)
(3)
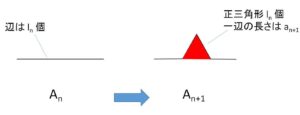
\(A_n\)に付け加える正三角形の一辺の長さは、\(A_{n+1}\)の一辺の長さ\(a_{n+1}\)だから、その面積は
\(\displaystyle\frac{1}{2}\{\displaystyle\frac{2}{\sqrt[4]{3}}(\displaystyle\frac{1}{3})^{n+1}\}^2\sin60°=(\displaystyle\frac{1}{3})^{2n+2}=\displaystyle\frac{1}{9}(\displaystyle\frac{1}{9})^{n}\)
付け加える正三角形の個数は\(A_n\)の辺の数\(l_n\)と等しいから、\(S_n\)に関する漸化式は
\(S_{n+1}=S_n+\displaystyle\frac{1}{9}(\displaystyle\frac{1}{9})^{n}×3\cdot4^n\)
よって
\(S_{n+1}=S_n+\displaystyle\frac{1}{3}(\displaystyle\frac{4}{9})^{n}\) (階差型)
\(S_0=1\) より、\(n≧1\) のとき
\(S_n=S_0+\displaystyle\sum_{\color{red}{k=0}}^{n-1}\displaystyle\frac{1}{3}(\displaystyle\frac{4}{9})^{k}\)
(初項は\(\displaystyle\frac{1}{3}\)、項数は\(n\)の等比数列の和)
\(S_n=1+\displaystyle\frac{1}{3}\cdot\displaystyle\frac{1-(\displaystyle\frac{4}{9})^n}{1-\displaystyle\frac{4}{9}}\)
したがって
\(S_n=\displaystyle\frac{8}{5}-\displaystyle\frac{3}{5}(\displaystyle\frac{4}{9})^n\)
(\(n=0\)でも成立)
以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→図形と数列・漸化式②(分割) back→条件式と帰納法