確率・場合の数と漸化式①(2項間・3項間)

確率・場合の数と漸化式の融合問題について見ていきます。

最初なので、まず問題文に漸化式を使うことの指示があるものを扱っていきます。
漸化式を立てる際には、2項間の場合では「\(n+1\)と\(n\)の関係」に着目し、\(n\)から\(n+1\)にどう状態が変化するのか考えるのが基本ですが、時には初手\(n=1\)についての場合分けを考えることもあります。

(例題1)
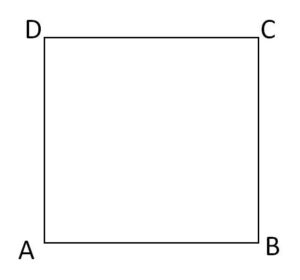
図のような正方形の4頂点\(A,B,C,D\)を次の規則で移動する動点\(Q\)がある。サイコロを振って\(1\)の目が出れば反時計回りに隣の頂点に移動し、\(1\)以外の目が出れば時計回りに隣の頂点に移動する。\(Q\)は最初\(A\)にあるものとし、\(n\)回移動した後の位置を\(Q_n\) (\(n=1,2,\cdots\)) とする。\(Q_{2n}=A\) である確率を\(a_n\)とおく。

確率漸化式① 例題1-1

(1)\(a_1\)を求めよ。
(2)\(a_{n+1}\)を\(a_n\)を用いて表せ。
(3)\(a_n\)を求めよ。

(解答)

\(a_1\)は\(Q_2=A\)である確率なので、2回の移動で\(Q\)が\(A\)にある確率です。\(Q\)の動き方は、\(A→D→A\) と \(A→B→A\) の場合しかありません。

(1)

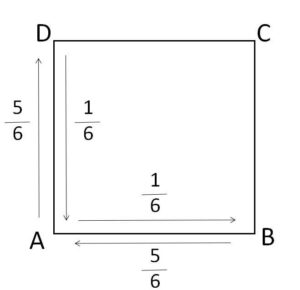
確率漸化式① 例題1-2

\(a_1\)は、\(Q_2=A\)である確率つまり2回の移動で\(Q\)が\(A\)にある確率である。
最初\(Q\)は\(A\)にあるので、動き方は \(A→D→A\), \(A→B→A\) の2通りだから

\(a_1=\displaystyle\frac{5}{6}\cdot\displaystyle\frac{1}{6}+\displaystyle\frac{1}{6}\cdot\displaystyle\frac{5}{6}\)

\(=\displaystyle\frac{5}{18}\)

(2)

1回の移動で隣に移動するので、偶数回の移動では\(A\)か\(C\)のどちらかにいます(奇数回では\(D\)or\(B\))。\(2n\)回の移動では\(A\)か\(C\)にいるので、\(2n\)回の移動で\(C\)にいる確率は\(1-a_n\)です。あとは\(a_{n+1}\)と\(a_n\)の関係式を導くだけです。

\(2n\)回の移動では\(Q\)は\(A\)か\(C\)にある。
\(a_{n+1}\)は \(2(n+1)=2n+2\)回の移動で\(Q\)が\(A\)にある確率で、\(2n+2\)回の移動で\(Q\)が\(A\)にあるのは

(ア)\(Q_{2n}=A\) のとき \(A→D→A\), \(A→B→A\) と動く
(イ)\(Q_{2n}=C\) のとき \(C→D→A\), \(C→B→A\) と動く

場合がある。\(Q_{2n}=C\) である確率は \(1-a_n\) だから

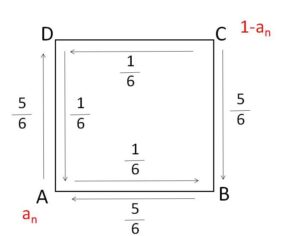
確率漸化式① 例題1-3

\(a_{n+1}=a_n(\displaystyle\frac{5}{6}\cdot\displaystyle\frac{1}{6}+\displaystyle\frac{1}{6}\cdot\displaystyle\frac{5}{6})+(1-a_n)(\displaystyle\frac{1}{6}\cdot\displaystyle\frac{1}{6}+\displaystyle\frac{5}{6}\cdot\displaystyle\frac{5}{6})\)

よって
\(a_{n+1}=-\displaystyle\frac{4}{9}a_n+\displaystyle\frac{13}{18}\)

(3)

漸化式を解くだけです。

(1)(2)より

\(a_1=\displaystyle\frac{5}{18}\)
\(a_{n+1}=-\displaystyle\frac{4}{9}a_n+\displaystyle\frac{13}{18}\)

特性方程式 \(x=-\displaystyle\frac{4}{9}x+\displaystyle\frac{13}{18}\) を解くと
\(x=\displaystyle\frac{1}{2}\) だから、漸化式は次のように変形できる。

\(a_{n+1}-\displaystyle\frac{1}{2}=-\displaystyle\frac{4}{9}(a_n-\displaystyle\frac{1}{2})\)

よって
\(a_n-\displaystyle\frac{1}{2}=(a_1-\displaystyle\frac{1}{2})(-\displaystyle\frac{4}{9})^{n-1}=-\displaystyle\frac{4}{18}(-\displaystyle\frac{4}{9})^{n-1}\)

\(=\displaystyle\frac{1}{2}(-\displaystyle\frac{4}{9})^{n}\)

したがって
\(a_n=\displaystyle\frac{1}{2}+\displaystyle\frac{1}{2}(-\displaystyle\frac{4}{9})^{n}\)

(例題2)
(1)階段を、下から一段ずつか一段おきに登る。階段が\(n\)段のときの登り方の総数を\(a_n\)通りとするとき、\(a_{n+2}\)を\(a_{n+1},a_{n}\)を用いて表せ。
(2)全部で\(11\)段ある階段を、下から一段ずつか一段おきに登る。登り方の総数を求めよ。

(解答)
(1)

階段が\(n+2\)段あるとき\(n+2\)段目に足をつけるのは、「\(n+1\)段目から1段登るか、\(n\)段目から2段登る(1段飛ばす)か」の2パターンしかありません。

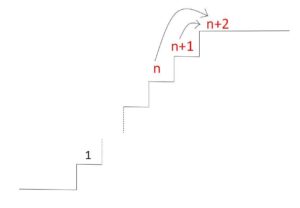
確率漸化式① 例題2

\(n+2\)段ある階段について\(n+2\)段目に到達するのは、「\(n+1\)段目から1段登るか、\(n\)段目から2段登る(1つ飛ばし)か」の場合がある。\(n+1\)段目に足をつけるときの登り方の総数は\(a_{n+1}\)通りで、\(n\)段目に足をつけるときも同様に\(a_n\)通りだから

\(a_{n+2}=a_{n+1}+a_{n}\)

(別解)
最初に1段登るか2段登るかに着目してもよいです。

最初に1段登るとき、残りは\(n+1\)段だから \(a_{n+1}\)通り
最初に2段登るとき、残りは\(n\)段だから \(a_n\)通り

よって
\(a_{n+2}=a_{n+1}+a_{n}\)

(2)

(1)で求めた3項間漸化式を解こうとすると、特性方程式 \(x^2-x-1=0\) の解が \(x=\displaystyle\frac{1±\sqrt{5}}{2}\) となるのでかえって複雑になってしまいます。したがって1個ずつ数値を代入して\(a_{11}\)を求めることになります。なおこの漸化式はフィボナッチ数列という数列の漸化式で(初期条件は少し違うが)、前2項の和がそのまま3つ目の項になっています。

1段の階段の登り方は1通りで \(a_1=1\)
2段の階段の登り方は、1段→1段または 2段(1つ飛ばし) の2通りだから \(a_2=2\)

\(a_{n+2}=a_{n+1}+a_{n}\)
より、\(a_3,a_4,\cdots\) と順に求めていくと

\(a_3=a_2+a_1=3\)
\(a_4=a_3+a_2=5\)
\(a_5=8\)
\(a_6=13\)
\(a_7=21\)
\(a_8=34\)
\(a_9=55\)
\(a_{10}=89\)
\(a_{11}=144\)

したがって\(11\)段の階段の登り方は\(144\)通り。

(補足)
仮に(1)の誘導がない場合には、漸化式を自分で立てるか直接計算するかになります。直接計算の方法としては、1段と2段の登り方をそれぞれ1,2として、数字1,2の並べ方を階段の登り方と対応させると、数字の並べ方の総数が登り方の総数になります。(例えば、 1,2,2,1,2,1,2 は1段→2段→2段・・・という登り方に対応)
2段登る回数は階段が全部で11段なので\(0,1,2,3,4,5\)回のいずれかで、それぞれの場合で並べ方を数えて総数を求めればよいです。

以上になります。お疲れさまでした。
ここまで見ていただきありがとうございました。
next→確率・場合の数と漸化式②　back→図形と数列・漸化式②