2つの確率変数の分布(同時分布)について見ていきます。
・同時分布
次の2つの袋
袋\(A:\)\(1,2,3\)の数字が書かれたカードが1枚ずつ入っている
袋\(B:\)赤、白、黒、青の\(4\)個のボールが1つずつ入っている
があるとき、確率変数\(X,Y\)を
\(X:\)\(A\)から1枚カード引いて出た数
\(Y:\)\(B\)から1個ボールを引いたとき出た赤いボールの数
とするとき、
\(P(X=a,Y=b)\) (\(a=1,2,3)\)、\((b=0,1)\)
について\(6\)つの確率を表にまとめると次のようになります。
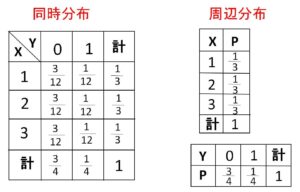
このような\((a,b)\)と確率\(P(X=a,Y=b)\)の対応関係を、\(X\)と\(Y\)の同時分布とよびます。同時分布は要するに2つの確率変数の分布をまとめて表したものです。
同時分布には次のような特徴があります。
(1)横方向(縦方向)の確率の和の合計が一番右(下)の計になる。
(2)さらに計を縦方向(横方向)で和をとると合計\(1\)になる。
よって同時分布は\(X,Y\)それぞれの確率分布を合わせたものと見ることができ、このそれぞれの確率分布は周辺分布とよばれます。周辺分布は\(X,Y\)の確率変数の分布を分けて表したものです。
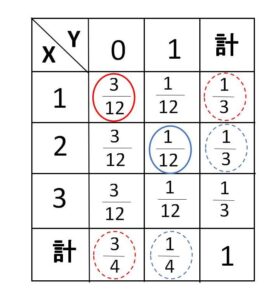
なお、右側の計の確率と下側の計の確率の積で全てのマスが作られている場合には、任意の\(a,b\)について
\(P(X=a,Y=b)=P(X=a)P(Y=b)\)
が成り立つことになるので、\(X,Y\)は独立となります。この例だと
\(Y=0\) について
\(\displaystyle\frac{3}{12}=\displaystyle\frac{1}{3}\cdot\displaystyle\frac{3}{4}\)
\(Y=1\) について
\(\displaystyle\frac{1}{12}=\displaystyle\frac{1}{3}\cdot\displaystyle\frac{1}{4}\)
となるので6マス全てで積の形に表すことができ、\(X,Y\)が独立であることが分かります。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→2変数の確率変数の期待値・分散 back→確率変数の独立