二項分布と期待値・分散

二項分布について見ていきます。

 

・二項分布
1個のサイコロを3回投げるとき、\(2\)の目が出る回数を確率変数\(X\)とおきます。
\(X\)のとり得る値は \(X=0,1,2,3\) であり、1回サイコロを投げて\(2\)の目が出る確率は\(\displaystyle\frac{1}{6}\)、\(2\)の目が出ない確率は\(\displaystyle\frac{5}{6}\)です。

よって反復試行の確率より、\(X=k\) (\(k=0,1,2,3\)) となる確率は
\(P(X=k)={}_3\mathrm{C}_{k}\left(\displaystyle\frac{1}{6}\right)^k\left(\displaystyle\frac{5}{6}\right)^{3-k}\)
で表され、\(X\)は次の確率分布に従います。

このような分布は、1回のサイコロを投げるという試行で
「事象\(A\)(\(2\)の目が出る)が 起こる か 起こらないか」
という単純な試行の結果がもとになっており、その確率変数\(X\)も事象\(A\)が起こる回数という単純なものです。

一般に、1回の試行で事象\(A\)の起こる確率が \(p\) (\(0<p<1\)) であるとき、この試行を\(n\)回行う反復試行において、\(A\)の起こる回数を確率変数\(X\)とすると、\(X\)は次のような分布に従います。

\(A\)が起こらない確率を\(q\)とすると、\(q=1-p\) であり

\(P(X=k)={}_n\mathrm{C}_{k}p^kq^{n-k}\)　(\(k=0,1,2,\cdots,n\))

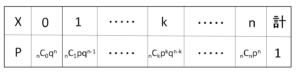
この確率分布を二項分布とよび、\(B(n,p)\) で表します(\(n\)回試行で、確率\(p\)で起こる事象の起こる回数の分布という意味)。最初の例だと \(B(3,\displaystyle\frac{1}{6})\) となります。
\(B\)は Binomial distribution (二項分布) の頭文字です。

なお \((p+q)^n\) を二項定理により展開すると

\((p+q)^n={}_n\mathrm{C}_{0}q^n+{}_n\mathrm{C}_{1}pq^{n-1}+\cdots+{}_n\mathrm{C}_{n}p^n\)

ですが、それぞれの項が各確率をちょうど表しています。また、\((p+q)^n=1^n=1\) より、確率の和が\(1\)になることも確認できます。

 

 

 

・二項分布の期待値・分散
二項分布の期待値・分散は、各試行において確率変数を設定することで(全部で\(n\)個の変数になる)、うまく求めることができます。先に結論から示すと次のようになります。

標準偏差は分散の正の平方根をとるだけなので省略します。

感覚的には、1回の試行での期待値と分散が
\(E_1=0\cdot(1-p)+1\cdot p=p\)、
\(V_1=0^2\cdot(1-p)+1^2\cdot p-p^2=p(1-p)\)
なので、全部ではこれらを\(n\)倍すればよいということですが、丁寧に証明すると次の通りになります。

(証明)
\(1\)回の試行で確率\(p\)で起こる事象を\(A\)とする。\(n\)回繰り返す反復試行において
「\(k\)回目の試行で\(A\)が起これば\(1\)、起きなければ\(0\)という値をとる確率変数を\(X_k\)」
とする。すると事象\(A\)が起こる回数\(X\)は
\(X=X_1+X_2+\cdots+X_n\)
で表すことができる。\(X_1,X_2,\cdots,X_n\)はすべて同じ確率分布に従い、ある回の事象の起き方は他の回の事象の起き方に影響しないので、\(n\)個の変数は互いに独立である。

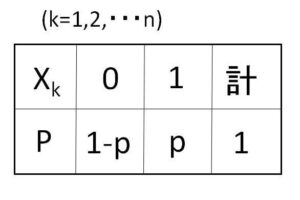
\(E(X_k)=0\cdot(1-p)+1\cdot p=p\)

\(V(X_k)=E(X_k^2)-\{E(X_k)\}^2\)
\(=0^2\cdot(1-p)+1^2\cdot p-p^2\)
\(=p(1-p)\)
だから

\(E(X)=E(X_1+X_2+\cdots+X_n)\)
\(=E(X_1)+E(X_2)+\cdots+E(X_n)\)
\(=p+p+\cdots+p\)
\(=np\)

\(V(X)=V(X_1+X_2+\cdots+X_n)\)
\(=V(X_1)+V(X_2)+\cdots+V(X_n)\)　(独立より)
\(=p(1-p)+p(1-p)+\cdots+p(1-p)\)
\(=np(1-p)\)
\(=npq\)

 

(参考)

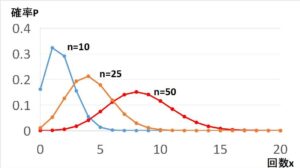
二項分布 \(B(n,\displaystyle\frac{1}{6})\) を折れ線グラフで表すと上記のようになります。
グラフは \(n=10,25,50\) の場合を合わせて表示していますが、それぞれの期待値(平均)は、
\(E(X)=np=\displaystyle\frac{1}{6}n\) より、
\(E(X)=\displaystyle\frac{10}{6},\displaystyle\frac{25}{6},\displaystyle\frac{50}{6}\)
となり、平均がどんどん大きくなっていき、グラフが右にシフトしていることに一致します。
また、\(n\)を大きくすると「左右対称の滑らかな山型のグラフ」に近づくことが予想されます。(これが正規分布になる)

 

 

(例題)
点\(P\)が数直線上を原点から出発して動く。硬貨を投げて表が出れば\(P\)は正の方向に\(2\)だけ動き、裏が出れば負の方向に\(1\)だけ動く。\(40\)回硬貨を投げたときの点\(P\)の座標を確率変数\(Y\)とする。

(1)表が出る回数を確率変数\(X\)とするとき、\(X\)の期待値・分散を求めよ。
(2) (1)を利用して\(Y\)の期待値・分散を求めよ。

 

(解答)
(1)

硬貨を1回投げて表が出る確率は\(\displaystyle\frac{1}{2}\)なので、\(X\)は二項分布 \(B(40,\displaystyle\frac{1}{2})\) に従う。
よって
\(E(X)=40\cdot\displaystyle\frac{1}{2}=20\)
\(V(X)=40\cdot\displaystyle\frac{1}{2}\cdot(1-\displaystyle\frac{1}{2})=10\)

(2)

題意より
\(Y=2X-(40-X)=3X-40\) だから

\(E(Y)=E(3X-40)=3E(X)-40\)
\(=3\cdot20-40\)
\(=20\)

\(V(Y)=V(3X-40)=3^2V(X)\)
\(=9\cdot10\)
\(=90\)

 

 

 

以上なります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→確率密度関数の性質　back→2変数の期待値・分散の例題