連続型確率分布の基本について見ていきます。
・連続型確率変数と確率密度関数
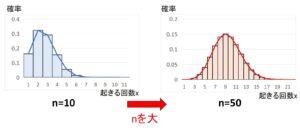
上図は、二項分布 \(B(n,p)\) の \(n=10,50\) における折れ線と棒グラフを合わせたものです。これを見ても分かる通り、\(n=50\) の方が折れ線グラフは滑らかで、全体に対する棒グラフの横幅も小さくなっています。よって、\(n\)を大きくするほど(確率に関する情報量が多いほど)、分布の形が1つの連続曲線に近づくことになります。
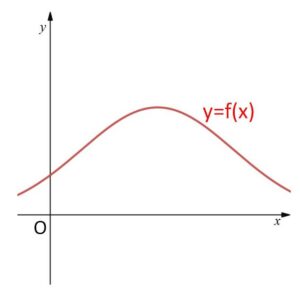
一般に、連続な値をとる確率変数\(X\)の確率分布を考える場合、\(X\)の分布を表す連続曲線
\(y=f(x)\) (連続関数)
を用います。この分布を表す曲線を分布曲線とよび、関数 \(y=f(x)\) を確率密度関数とよびます。(確率密度関数とわざわざよぶ理由は後に説明します)
また、このような連続な値をとる変数\(X\)を連続型確率変数とよび、これに対して二項分布のようなとびとびの値をとる変数\(X\)を離散型確率変数とよびます。
連続型の確率分布はより情報量の多い分布になっているだけでなく、\(y=f(x)\) で表されることで微積分のような処理も可能になり、幅広く用いられることになります。
上記二項分布のグラフでは、「縦軸が確率で、棒グラフの横軸が\(1\)であることから長方形の面積が確率そのもの」になっていて、これに対応させるように確率密度関数には次のような性質(定義)があります。
(1)常に \(f(x)≧0\)
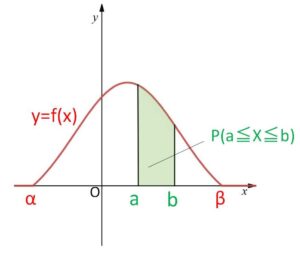
(2)確率は面積で表される。つまり
\(P(a≦X≦b)=\displaystyle\int_{a}^{b}f(x)dx\)
特に1点における確率は面積が\(0\)だから
\(P(X=a)=0\)
(3)全確率は\(1\)だから、定義域が \(α≦x≦β\) のとき
\(\displaystyle\int_{α}^{β}f(x)dx=1\)
(解説)
(1)積分したときに確率が負にならないように、\(0\)以上の条件がつきます。
(2)縦軸そのものの和をとると、\(x\)が連続的な変数であるために、膨大な値になってしまいます。そこで縦軸が確率そのものを表してるわけではなく、面積が確率を表すことになっています。これが確率密度関数とよばれる所以です。\(0\)でない確率をとるためには範囲を設定する必要があり、ある1つの値をとる確率 \(P(X=a)\) は面積が\(0\)により \(P(X=a)=0\) です。
(3)全確率が\(1\)になるように、確率密度関数の定義域全体で積分すると\(1\)になります。よってもし確率密度関数に未知係数がある場合には、定義域全体で積分して\(1\)になるように決定することになります。
(例題)
連続型確率変数\(X\)の確率密度関数が、\(a\)を定数とし
\(f(x)=a(1-x^2)\) (\(-1≦x≦1\))
で与えられている。
(1)定数\(a\)の値を求めよ。
(2)\(\displaystyle\frac{1}{2}≦X≦1\) となる確率を求めよ。
(解答)
(1)
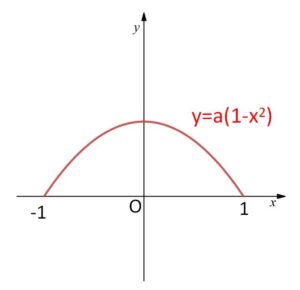
\(\displaystyle\int_{-1}^{1}a(1-x^2)dx=1\) だから
\(2a\left[x-\displaystyle\frac{1}{3}x^3\right]_{0}^{1}=1\) (偶関数)
\(\displaystyle\frac{4}{3}a=1\)
よって
\(a=\displaystyle\frac{3}{4}\)
(2)
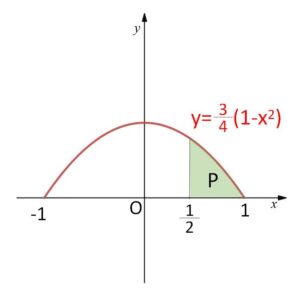
\(P(\displaystyle\frac{1}{2}≦X≦1)=\displaystyle\int_{\frac{1}{2}}^{1}\displaystyle\frac{3}{4}(1-x^2)dx\)
\(=\displaystyle\frac{3}{4}\left[x-\displaystyle\frac{1}{3}x^3\right]_{\frac{1}{2}}^{1}\)
\(=\displaystyle\frac{5}{32}\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→確率密度関数と期待値・分散・標準偏差 back→2項分布と期待値・分散