正規分布について見ていきます。
・二項分布の正規分布近似
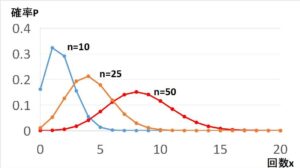
上記グラフは、二項分布 \(B(n,\displaystyle\frac{1}{6})\) の \(n=10,25,50\) を合わせて表示したものですが、\(n\)を大きくしていくと左右対称の山型のグラフに近づくことが分かります。この山型のグラフを正規分布とよびます。
一般に、確率変数\(X\)が二項分布 \(B(n,p)\) に従う場合
「\(n\)が十分大きいとき、\(X\)は近似的に 期待値\(np\)、分散\(np(1-p)\) の正規分布に従う」ことが言えます。\(n\)の大きさの基準は明確には決まっていませんが、\(n≧30\) が目安です。
これらの事は、もちろん上記のグラフと対応させて暗記してしまってもよいですが、中心極限定理を用いれば証明も可能です。(→二項分布の正規分布近似の証明)
世の中にあるデータの分布は正規分布であることが多く、テストの点数、身長や体重、工場で作られた食品の内容量、野菜などの農作物の重さなどがその例です。また統計の学問上でも最も基本的な分布になっていてよく利用されます。
・正規分布の確率密度関数
\(X\)が期待値\(m\)、分散\(σ^2\)である正規分布に従うとき、
\(E(X)=m\)、\(V(X)=σ^2\)、\(σ(X)=σ\)
であり、その正規分布は \(N(m,σ^2)\) で表されます。\(N\)は Normal distribution (正規分布) の頭文字です。
よって、上記二項分布を近似する正規分布は \(N(np,np(1-p))\) で表されます。
ところで、正規分布 \(N(m,σ^2)\) の確率密度関数は次のように表されることが知られています。(式は細かくは覚えなくてよいです)
\(f(x)=\displaystyle\frac{1}{\sqrt{2π}σ}e^{-\frac{(x-m)^2}{2σ^2}}\)・・・①
\(e\)はネイピア数とよばれる無理数の定数で、具体的な値は \(e=2.718\cdots\) です(数Ⅲ)。変数\(x\)以外の文字は全て\(x\)に対して定数なので、関数①は指数関数です。①のグラフの形を決める部分は \(e^{-\frac{(x-m)^2}{2σ^2}}\) であり、係数\(\displaystyle\frac{1}{\sqrt{2π}σ}\)で面積が全部で\(1\)になるように調整されています。(①の積分は高校範囲外)
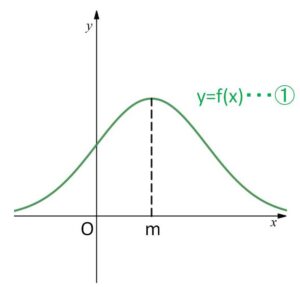
正規分布の確率密度関数①には次のような特徴があります。
(1)
\(x=m\) (期待値) について対称。(左右対称)
これは
\(f(m+x’)=f(m-x’)\)
が成り立つことから分かる。
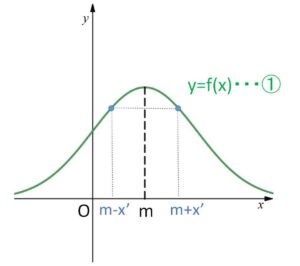
(2)
\(f(x)\)の\(e\)の指数が\(0\)以下の値をとることから、
\(x=m\) で最大値をとり、\(x=m\) から遠ざかるにつれて減少して、次第に\(0\)に近づく。(山型となる)
(3)
\(f(m)=\displaystyle\frac{1}{\sqrt{2π}σ}e^{0}\) と、標準偏差\(σ\)が散らばりを表していることから、
\(σ\)が大きくなると、最大値が小さくなって横に広がり、平たい山型になる。\(σ\)が小さくなると、最大値が大きなって、\(x=m\) 付近に集中するので鋭い山型になる。
(微分(数Ⅲ)を利用して検討してもよいです)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→標準正規分布 back→確率密度関数の期待値・分散・標準偏差