正規分布に関する例題

正規分布や二項分布の近似に関する例題です。
標準正規分布に帰着させることがポイントです。

(例題1)
ある食品\(F\)を摂取したときに、血液中の物質\(A\)の量がどのように変化するか調べたい。食品摂取前と摂取してから\(3\)時間後に、それぞれ一定量の血液に含まれる物質\(A\)の量(単位は\(m\mathrm{g}\))を測定し、その変化量、すなわち摂取後の量から摂取前の量を引いた値を表す確率変数を\(X\)とする。\(X\)は正規分布に従い、期待値と標準偏差はそれぞれ \(E(X)=-7\)、\(σ(X)=5\) とする。

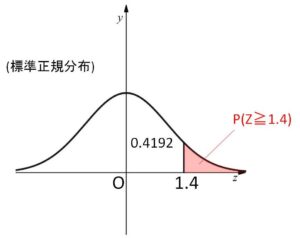
このとき、食品\(F\)を摂取したときに物質\(A\)の量が減少しない確率 \(P(X≧0)\) を求めよ。ただし確率変数\(Z\)が標準正規分布に従うとき、\(P(0≦Z≦1.4)=0.4192\) である。

(解答)
\(Z=\displaystyle\frac{X-(-7)}{5}=\displaystyle\frac{X+7}{5}\)
は標準正規分布に従う。

よって
\(X≧0\) のとき \(\displaystyle\frac{X+7}{5}≧1.4\) だから

\(P(X≧0)=P(Z≧1.4)\)
\(=0.5-P(0≦Z≦1.4)\)　(対称性から右半分の面積は\(0.5\))
\(=0.5-0.4192\)
\(=0.0808\)   (約\(8％\))

(例題2)
\(a\)を\(3\)以上の正の整数とする。\(2,4,6,\cdots,2a\) の数字がそれぞれ一つずつ書かれた\(a\)枚のカードが箱に入っている。この箱から\(3\)枚のカードを同時に取り出し、それらのカードを横\(1\)列に並べる。この試行において、カードの数字が左から小さい順に並んでいる事象を\(A\)とする。

(1)事象\(A\)の起こる確率を求めよ。
(2)この試行を\(180\)回繰り返し、事象\(A\)が起こる回数を表す確率変数を\(X\)とする。\(X\)はある分布に従うが、この分布の名称を答えよ。
(3)\(X\)の平均と標準偏差を求めよ。
(4)事象\(A\)が\(18\)回以上\(36\)回以下起こる確率の近似値を求めたい。試行回数\(180\)は十分大きいことから、\(X\)は近似的にある分布に従う。この分布の名称を答えよ。またこの分布の平均と標準偏差を求めよ。
(5) (4)の近似値 \(P(18≦X≦36)\) を求めよ。ただし確率変数\(Z\)が標準正規分布に従うとき、\(P(0≦Z≦1.2)=0.3849\)、\(P(0≦Z≦2.4)=0.4918\) である。

(解答)
(1)

選んだ\(3\)枚のカードは常に違う数字になる。よって、\(3\)枚のカードの並べ方が\(3!\)通りであり、そのうち左から小さい順に並ぶのは\(1\)通りだから、求める確率\(p\)は
\(p=\displaystyle\frac{1}{6}\)

(別解)
\(a\)枚のカードから\(3\)枚のカードを選んで並べるのは、\({}_a\mathrm{P}_3\) 通り。
このうち、左から小さい順に並ぶのは\(a\)個の異なる数から\(3\)個の異なる数を選ぶ組み合わせの数と同じだから、\({}_a\mathrm{C}_3\) 通り。
よって確率\(p\)は
\(p=\displaystyle\frac{{}_a\mathrm{C}_3}{{}_a\mathrm{P}_3}=\displaystyle\frac{\displaystyle\frac{a(a-1)(a-2)}{3!}}{a(a-1)(a-2)}\)
\(=\displaystyle\frac{1}{6}\)

(2)
\(1\)回の試行で事象\(A\)が起こる確率は\(\displaystyle\frac{1}{6}\)、起こらない確率は\(\displaystyle\frac{5}{6}\)。\(X\)は試行を\(180\)回繰り返した際の事象\(A\)が起こる回数なので、\(X\)は二項分布\(B(180,\displaystyle\frac{1}{6})\)に従う。

(3)
\(X\)は \(B(180,\displaystyle\frac{1}{6})\) に従うので
\(E(X)=180\cdot\displaystyle\frac{1}{6}=\)\(30\)
\(σ(X)=\sqrt{180\cdot\displaystyle\frac{1}{6}\cdot(1-\displaystyle\frac{1}{6})}=\sqrt{25}=\)\(5\)

(4)
試行回数 \(n=180\) は十分大きいので、二項分布 \(B(180,\displaystyle\frac{1}{6})\) は近似的に正規分布に従うことになる。その平均と標準偏差は二項分布のそれと同じだから、平均は\(30\)、標準偏差は\(5\)。 (この正規分布は\(N(30,25)\)になる)

(5)
(4)の結果から
\(Z=\displaystyle\frac{X-30}{5}\)
で表される\(Z\)は、標準正規分布に従う。

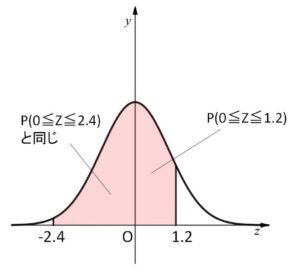
\(18≦X≦36\) のとき
\(-2.4≦\displaystyle\frac{X-30}{5}≦1.2\)
となるから

\(P(18≦X≦36)\)
\(=P(-2.4≦Z≦1.2)\)
\(=P(0≦Z≦2.4)+P(0≦Z≦1.2)\)　(対称性より)
\(=0.4918+0.3849\)
\(=0.8767\)

※(4)(5)の近似について
理屈上では、\(X=18,19,\cdots,36\) の場合のすべての確率を求めて(反復試行の確率で求まる)、和をとれば近似値でない確率が計算できます。しかしこれは大変なので正規分布による近似を行って近似値を求めるという流れをとっています。

以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→推測統計の概要　back→標準正規分布