標本平均について見ていきます。
そこで、抽出した標本について平均値を計算すればよさそうですが、実はそれは正解です。その平均は標本平均と呼ばれますが、この標本平均は統計的な推測でとても重要な確率変数になっています。
・標本平均とその期待値・分散・標準偏差
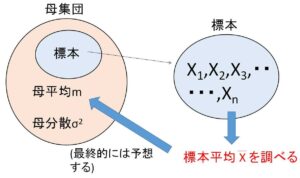
母集団から、大きさ\(n\)の標本を無作為抽出するとき、その\(n\)個の個体の変量の値をそれぞれ\(X_1,X_2,\cdots,X_n\) とします(どの個体を抽出するか分からないので変数を設定する)。これらの標本を1組のデータとするとき、その平均値
\(\overline{X}=\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\)
を標本平均とよびます。\(X_1,X_2,\cdots,X_n\)はいずれも確率変数なので、標本平均\(\overline{X}\)も確率変数です。
よって標本平均の期待値と分散・標準偏差も計算でき、その結果は次のようになります。
母平均・母分散・母標準偏差を\(m,σ^2,σ\)とすると
\(E(\overline{X})=m\)
\(V(\overline{X})=\displaystyle\frac{σ^2}{n}\)、\(σ(\overline{X})=\displaystyle\frac{σ}{\sqrt{n}}\)
(ただし、分散・標準偏差については復元抽出、または復元抽出とみなせる場合)
(解説)
これらの意味する内容や注意点は後で説明することにして、ひとまず証明から始めたいと思います。
(証明)
期待値について
\(E(\overline{X})=E\left(\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\right)\)
\(=\displaystyle\frac{1}{n}E(X_1+X_2+X_3+\cdots+X_n)\)
\(=\displaystyle\frac{1}{n}\{E(X_1)+E(X_2)+\cdots+E(X_n)\}\)
(各変数については大きさ\(1\)の標本。よって
\(m=E(X_1)=E(X_2)=\cdots=E(X_n)\) より)
\(=\displaystyle\frac{1}{n}(m+m+\cdots+m)\)
\(=\displaystyle\frac{n\cdot m}{n}\)
\(=m\)
分散について
\(V(\overline{X})=V\left(\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\right)\)
\(=\displaystyle\frac{1}{n^2}V(X_1+X_2+\cdots+X_n)\)
ここで、復元抽出または復元抽出とみなせる場合、\(X_1,X_2,\cdots,X_n\)は互いに独立だから
\(V(\overline{X})\)
\(=\displaystyle\frac{1}{n^2}\{V(X_1)+V(X_2)+\cdots+V(X_n)\}\)
(\(σ^2=V(X_1)=V(X_2)=\cdots=V(X_n)\) より)
\(=\displaystyle\frac{1}{n^2}(σ^2+σ^2+\cdots+σ^2)\)
\(=\displaystyle\frac{n\cdotσ^2}{n^2}\)
\(=\displaystyle\frac{σ^2}{n}\)
正の平方根をとれば標準偏差が得られる。
(注意点)
(1)これらの等式は\(n\)の大きさに制限はない。(小さくてもよい)
(2)まだこの段階では標本平均\(\overline{X}\)の分布がどうなるかまでは言及してない。(もちろん\(n\)が大きい場合は中心極限定理より正規分布に近似的に従うことにはなるが)
(標本平均の期待値・分散・標準偏差の表す意味)
例として日本人男性全員を母集団として、その身長について検討します。
\(100\)人標本を抽出することにして調査をし、その結果から標本平均を計算すると、
\(\overline{X}=171.3 (cm)\)
また別の機会に\(100\)人標本を抽出して、標本平均を計算すると
\(\overline{X}=170.4 (cm)\)
と得られたとします。
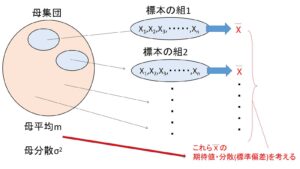
現実の調査では1回もしくはある程度の回数しか行わないですが、これを仮に何度も繰り返すことにすると、色々な標本平均\(\overline{X}\)が得られ、これらの\(\overline{X}\)は何かしらの分布に従うことになり、この平均値(期待値)が\(E(\overline{X})\)の表す意味です。(ややこしい言い方をすると \(E(\overline{X})\)は標本平均の平均になるので、平均の平均ということになります)
分散\(V(\overline{X})\)もこの何かしらの分布の分散(散らばり)ですが、\(n\)が大きいほど(1回の調査での標本の数が大きいほど)その標本平均は真の平均(母平均)に近づくと考えれられるので、繰り返しの調査で得られる標本平均は母平均に近いものが多くなるので、分散は\(n\)が大きいほど小さくなると考えれられます。それが \(V(\overline{X})=\displaystyle\frac{σ^2}{n}\) の分母に表されています。
標準偏差も散らばりを表す量なので、こちらも分母に\(n\)が登場しています。(\(σ(\overline{X})=\displaystyle\frac{σ}{\sqrt{n}}\) )
(例題)
ある大学には多くの留学生が在籍している。この大学の留学生に対して学習や生活を支援する留学生センターでは、留学生の日本語の学習状況について関心を寄せている。
そこで、この大学の\(40\)人の留学生を無作為に抽出し、ある\(1\)週間における留学生の授業以外の自主的な日本語学習時間(分)を調査した。ただし、この大学の留学生全員を母集団とするとき、日本語の自主的な学習時間は母平均\(m\)、母分散\(σ^2\)の分布に従うものとする。
\(σ^2=640\) と仮定するとき、標本平均の標準偏差を求めよ。
(解答)
\(40\)人の日本語学習時間をそれぞれ、\(X_1,X_2,\cdots,X_{40}\) とすると、その標本平均は
\(\overline{X}=\displaystyle\frac{X_1+X_2+\cdots+X_{40}}{40}\)
\(\overline{X}\)の標準偏差は
\(σ(\overline{X})=\displaystyle\frac{σ}{\sqrt{40}}\)
\(σ^2=640\) より
\(σ(\overline{X})=\displaystyle\frac{\sqrt{640}}{\sqrt{40}}\)
\(=4\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→中心極限定理・大数の法則 back→復元抽出と非復元抽出