中心極限定理や大数の法則について見ていきます。
・中心極限定理
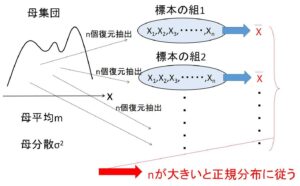
母平均・母分散・母標準偏差が\(m,σ^2,σ\)であるこの母集団(正規分布とは限らない)から、大きさ\(n\)の無作為標本を抽出するとき、標本平均 \(\overline{X}=\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\) の期待値・分散・標準偏差は(復元抽出の場合)
\(E(\overline{X})=m\)、\(V(\overline{X})=\displaystyle\frac{σ^2}{n}\)、\(σ(\overline{X})=\displaystyle\frac{σ}{\sqrt{n}}\)
で表されました。この\(\overline{X}\)について分布まで検討したのが中心極限定理です。中心極限定理によれば、復元抽出または復元抽出とみなせる場合、標本の大きさ\(n\)が十分大きいとき、標本平均\(\overline{X}\)が近似的に期待値\(m\)、分散\(\displaystyle\frac{σ^2}{n}\) の正規分布 \(N(m,\displaystyle\frac{σ^2}{n})\) に従います。
確率変数\(X_1,X_2,\cdots,X_n\)は互いに独立で、平均値が\(m\)、分散が\(σ^2\)の同じ分布に従うものとする。このとき標本平均\(\overline{X}=\displaystyle\frac{X_1+X_2+\cdots+X_n}{n}\)を標準化した
\(Z=\displaystyle\frac{\overline{X}-m}{\displaystyle\frac{σ}{\sqrt{n}}}\)
は、\(n\)が十分大きいとき近似的に標準正規分布に従う。
証明は高校範囲外なので結論だけ覚えて下さい。この定理により\(\overline{X}\)が正規分布 \(N(m,\displaystyle\frac{σ^2}{n})\) に従うことが分かります。問題を解く際には最終的に標準正規分布表を利用することになるので、標準化したほうで覚えておくとよいと思います。
十分大きい\(n\)の明確な基準はありませんが、目安は\(n≧30\)です。
各変数\(X_1,X_2,\cdots,X_n\)を同じ母集団から抽出した\(n\)個の標本の変量に対応する変数とすると、復元抽出のとき\(X_1,X_2,\cdots,X_n\)は互いに独立で、1つ1つはいずれも大きさ\(1\)の標本なので母集団と同じ平均値が\(m\)、分散が\(σ^2\)の同じ分布に従い、中心極限定理が適用できます。
(中心極限定理の表す意味)
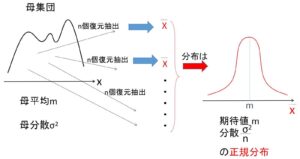
例えば母集団を日本人男性全員として、\(n=100\) とすれば
1回目の調査で\(100\)人を抽出し標本平均を計算すると
\(\overline{X}=171.2(cm)\)
2回目の調査で\(100\)人を抽出し標本平均を計算すると
\(\overline{X}=170.5(cm)\)
実際の調査では調査は1回かある程度の回数になりますが、これを何度も繰り返してデータを集めると\(\overline{X}\)はある分布に従うことになりますが、\(n\)(標本の数)が大きい場合にはこの分布は正規分布である言っているのが中心極限定理です。
この定理のすごいところは\(n\)が十分大きいなどの条件はありますが、もとの母集団の分布の形状によらず標本平均が正規分布に従うという点です。標本平均\(\overline{X}\)が正規分布に従うことにより、逆算的に母平均\(m\)を予想(推定)することができ、これが母平均の推定になります。
(注)
中心極限定理は母集団の分布によらない定理ですが、母集団の分布が正規分布である場合は、\(n\)の大きさに関わらず標本平均は正規分布に従います。これも証明は高校範囲外ですが、知識として知っておくとよいでしょう。
・大数の法則
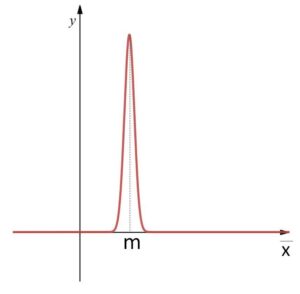
抽出する標本の大きさ\(n\)をどんどん大きくしていくと、散らばりを表す分散\(\displaystyle\frac{σ^2}{n}\)が\(0\)に近づくので、中心極限定理も踏まえると、標本平均の分布は期待値\(m\)に集中する正規分布になってきます。よって、\(n\)が極めて大きい場合には\(\overline{X}\)はほとんど\(m\)、つまり母平均に近づくことが分かります。これを大数の法則とよびます。(たいすうと読む。だいすうではない)
母平均\(m\)の母集団から大きさ\(n\)の無作為標本を抽出するとき、その標本平均\(\overline{X}\)は、\(n\)が大きくなるに従って母平均\(m\)に近づく。
感覚的にも、標本の個数\(n\)を多くとればとるほど標本平均は真の平均(母平均)に近づきそうなのは分かると思います。
中心極限定理の行き着く先が大数の法則であり、逆に言えば大数の法則の議論になるような\(n\)までの途中経過が中心極限定理で示す内容となります。
(例題)
\(P\)大学生の1日あたりの読書時間の平均と標準偏差は、母平均\(24\)分、母標準偏差\(40\)分である。\(P\)大学生から\(400\)人を標本として無作為抽出した。
(1)標本平均の期待値と標準偏差を求めよ。
(2)標本の大きさ\(400\)は十分に大きいので、標本平均の分布は正規分布に近似できる。このことを利用して、標本平均が\(30\)分以上となる確率を求めよ。なお\(Z\)が標準正規分布に従うとき、\(P(0≦Z≦3)=0.4987\) である。
(解答)
(1)
\(E(\overline{X})=24\) (分)
\(σ(\overline{X})=\displaystyle\frac{40}{\sqrt{400}}=2\) (分)
(2)
\(Z=\displaystyle\frac{\overline{X}-24}{2}\)
は標準正規分布に従う。
\(X≧30\) のとき \(\displaystyle\frac{X-24}{2}≧3\) だから
\(P(X≧0)=P(Z≧3)\)
\(=0.5-P(0≦Z≦3)\) (標準正規分布で右半分を考える)
\(=0.5-0.4987\)
\(=0.0013\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→母比率と標本比率 back→標本平均の期待値・分散・標準偏差