標本平均から母平均を推定する方法について見ていきます。
・母平均の推定
母集団から大きさ\(n\)の無作為標本を抽出するとき、\(n\)が十分に大きい場合には標本平均\(\overline{X}\)は近似的に正規分布に従います。このことを利用して逆算的に母平均\(m\)がどの範囲に存在するかを推測することができます。これを母平均の推定といいます。
母平均を\(m\)、母標準偏差を\(σ\)とすると標準化した
\(Z=\displaystyle\frac{\overline{X}-m}{\displaystyle\frac{σ}{\sqrt{n}}}\)・・・①
は標準正規分布に従います。ここで正規分布のグラフと\(z\)軸の間の面積は確率を表していることから、\(Z\)(母平均\(m\)を含む式)に関する確率的な不等式を立てることができます。
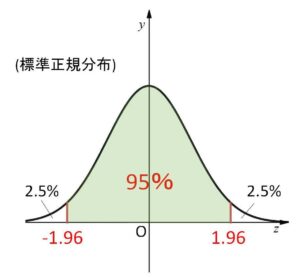
例えば確率\(0.95\)(\(95%\))を選ぶことにします。標準正規分布のグラフが左右対称であることと\(m\)が範囲に含まれるように、中心から対称に面積が\(0.95\)になるように考えると
\(0.95÷2=0.475\)、\(P(0≦Z≦1.96)=0.475\)
なので
\(P(-1.96≦Z≦1.96)=0.95\)・・・②
です。
②に①を代入すると
\(P\left(-1.96≦\displaystyle\frac{\overline{X}-m}{\displaystyle\frac{σ}{\sqrt{n}}}≦1.96\right)=0.95\)
母平均\(m\)を推定したいので\(m\)について整理していくと
\(P\left(-1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}≦\overline{X}-m≦1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}\right)=0.95\)
\(P\left(-\overline{X}-1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}≦-m≦-\overline{X}+1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}\right)=0.95\)
よって
\(P\left(\overline{X}-1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}≦m≦\overline{X}+1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}\right)=0.95\)・・・③
が成り立ちます。
③の括弧内の不等式の各変数については、標本平均\(\overline{X}\)は調査の結果から分かり、\(n\)は標本の大きさなので分かり、よって残りの母標準偏差\(σ\)が分かれば\(m\)の不等式が具体的な数値で表されることになります。問題では\(σ\)は与えられることが多いですが、実際の調査では\(σ\)は分からないことも多いので、その際には標本標準偏差で代用することになります。(次回扱います)
さて③は、母平均\(m\)が区間
\(\overline{X}-1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}≦x≦\overline{X}+1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}\)
の範囲に存在する確率が\(95%\)であることを意味しているので、この区間を母平均\(m\)に対する信頼度\(95%\)の信頼区間とよびます。
同様に
\(P(-2.58≦Z≦2.58)=0.99\)・・・(注)
であることから、上記の\(1.96\)を\(2.58\)に変えるだけで信頼度\(99%\)の信頼区間を求めることができます。(その他の信頼度についても同様ですが、主にこの2種類が扱われます)
信頼度、つまり母平均\(m\)が区間に入っている確率を上げるにはその区間が広がることになりますが、それが \(1.96 \to 2.58\) という数値に現れています。実際に応用する際には、区間の広さと信頼度を天秤にかけて信頼度を調整することなります。
(注)\(2.58\)について
\(0.99÷2=0.495\)であり、また標準正規分布表によると
\(P(0≦Z≦2.57)=0.4949\)
\(P(0≦Z≦2.58)=0.4951\)
なので、これだけだと\(2.57,2.58\)のどちらをとればよいか分からない。しかし\(0.4949,0.4951\)は近似値なので小数第\(5\)位以下を考えるとそれぞれ \(0.49492,0.49506\) であり、\(0.4950\)に近いのは \(Z=2.58\) となる。
・信頼度\(P%\)の信頼区間の意味
信頼度\(95%\)を例にします。
\(\overline{X}-1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}≦m≦\overline{X}+1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}\)
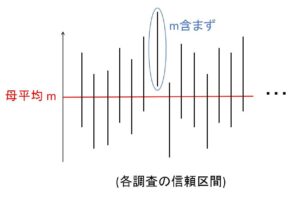
は、母標準偏差\(σ\)を既知とすれば、抽出した標本の結果より具体的な範囲を表します。実際に調査をするのは\(1\)回か数回程度になると思いますが、「大きさ\(n\)の標本を抽出し標本平均を求める」という操作を仮に\(100回\)行ったとします。すると基本的には調査の結果は毎回変わってくるので、異なる信頼区間が\(100\)個得られることになります。これら区間のうち\(95\)個程度は母平均\(m\)を含んでいるということが信頼度\(95%\)の信頼区間の表す意味です。
調査の結果が基本的に毎回異なるので、確率的に\(m\)が含まれる区間を表すことになるのです。
(例題)
ある大学には多くの留学生が在籍している。この大学の留学生センターは、ある1週間における留学生の自主的な日本語学習時間(分)を調査した。この大学の留学生全体を母集団とすると、自主的な日本語学習は母平均\(m\)、母分散\(640\)の分布に従う。
\(40\)人の留学生を無作為に抽出したところ、調査の結果は\(40\)人の学習時間の平均値は\(120\)だった。標本平均が近似的に正規分布に従うとして、母平均\(m\)に対する信頼度\(95%\)の信頼区間 \(C_1≦m≦C_2\) を求めよ。
(解答)
\(\overline{X}-1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}≦m≦\overline{X}+1.96\cdot\displaystyle\frac{σ}{\sqrt{n}}\)
\(\overline{X}=120\)、\(σ=\sqrt{640}\)、\(n=40\) を代入すると
\(120-1.96\cdot\displaystyle\frac{\sqrt{640}}{\sqrt{40}}≦m≦120+1.96\cdot\displaystyle\frac{\sqrt{640}}{\sqrt{40}}\)
\(120-1.96\cdot4≦m≦120+1.96\cdot4\)
よって
\(112.16≦m≦127.84\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→母平均の推定②(分散未知) back→母比率と二項分布