仮説検定の過誤について整理します。
・仮説検定の過誤
有意水準\(5%\)で検定をするとき、\(5%\)以下の確率で起きることは稀なケースであると判断をしますが、逆に言うと帰無仮説が正しい場合であっても\(5%\)以下の確率で起きえてしまう事です。そこでこの有意水準は帰無仮説が正しい場合であっても間違って棄却されてしまう確率を表していることから危険率とも呼ばれます。またこの「帰無仮説が正しい場合に間違って棄却してしまう」ことを第一種の過誤といいます。
一方、「帰無仮説が間違っている場合に棄却しない」過誤もあり、これを第二種の過誤といいます。
第一種の過誤の確率を減らすには有意水準を下げればよいですが、下げれば下げるほど帰無仮説が棄却されにくくなるので第二種の過誤の確率が増えることになります。

もう少し第一種の過誤と第二種の過誤について母平均の検定をもとに検討してみます。
帰無仮説で設定した母平均を\(m\)、真実の母平均を\(m_r\)とすれば
(第一種の過誤)
帰無仮説は正しいので \(m=m_r\) となり
\(Z=\displaystyle\frac{\overline{X}-m}{\displaystyle\frac{σ}{\sqrt{n}}}=\displaystyle\frac{\overline{X}-m_r}{\displaystyle\frac{σ}{\sqrt{n}}}\)
が近似的に従う分布は標準正規分布そのものになります。
よって、第一種の過誤が起こる確率\(α\)は有意水準(危険率)と同じです。
(第二種の過誤)
帰無仮説が正しくないので \(m≠m_r\) であり
\(Z=\displaystyle\frac{\overline{X}-m}{\displaystyle\frac{σ}{\sqrt{n}}}\)
が近似的に従う分布は正規分布ですが、標準正規分布よりズレたものになります。
このズレは\(m\)と\(m_r\)のズレなので、第二種の過誤が起こる確率はケースバイケースになりますが、ズレが大きいほど第二種の過誤が起こる確率は低くなります(帰無仮説が棄却されやすくなる)。
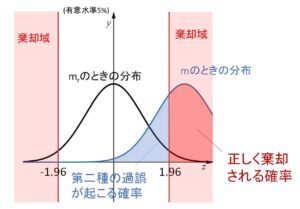
正しく棄却される確率は検出力ともよばれます。
第二種の過誤が起こる確率を\(β\)とすると、検出力は\(1-β\)です。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
back→母平均・母比率の検定