・絶対値
実数aに対して、数直線上で原点からの点aまでの距離をaの絶対値といい、|a|で表します。\(a\)の正負で場合分けすると、次のように定義されます。
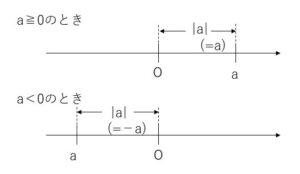
\(a≧0\)のとき、\(|a|=a\)
\(a<0\)のとき、\(|a|=-a\)
\(a<0\)のとき、\(|a|=-a\)
距離なので、座標が\(0\)以上の場合はそのまま記号がはずれ、座標が負の値の場合にははずす際にマイナスがつくことになります。
(例:\(|3|=3\), \(|-5|=-(-5)=5\))
絶対値について以下の性質が成り立ちます。
(1) \(|a|≧0\) (\(|a|=0\)となるのは \(a=0\)に限る)
(2) \(|a|=|-a|\)
(1)距離なので必ず0以上の値になります。
(2)は座標\(a\)と\(-a\)は原点について対称です。(原点までの距離が同じになります)
・2点間の距離
数直線上で、2点\(A(a), B(b)\) の距離は \(|b-a|\)で表されます。上記(3)より\(|a-b|\)とも表されます。\(a\)と\(b\)の大小は関係ありません。(図を参照して下さい)
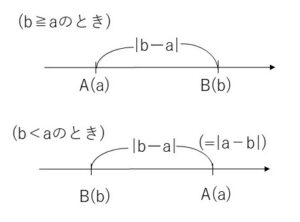
(例)\(A(2),B(-5)\)の距離は,\(|-5-2|=|-7|=7\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。