数直線上の2点間の距離と、2点の内分・外分点について学んでいきます。
・数直線上の2点間の距離
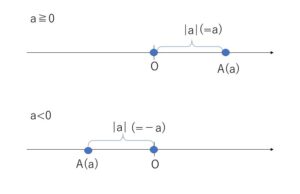
数直線上の点\(A(a)\)と原点\(O\)の間の距離を実数\(a\)の絶対値といい、\(|a|\)と表します。つまり
\(OA=|a|\)
\(a≧0\)のとき \(OA=a\)
\(a<0\)のとき \(OA=-a\) なので \(|a|\)は次のようになります。
\(|a|=a\) (\(a≧0\)), \(|a|=-a\) (\(a<0\))
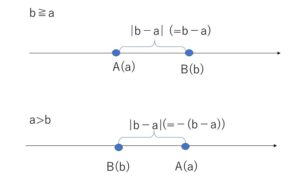
また、数直線上の2点\(A(a)\),\(B(b)\)間の距離を考えると
\(b≧a\) (\(b-a≧0\))のとき \(AB=b-a\)
\(a>b\) (\(b-a<0\))のとき \(AB=a-b=-(b-a)\)
なので
\(AB=|b-a|\)
・数直線上の2点の内分点・外分点
以下\(m,n\)を正の数とします。
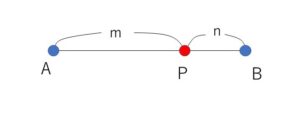
点\(P\)が線分\(AB\)上にあって
\(AP:PB=m:n\)
が成り立つとき、点\(P\)は\(AB\)を\(m:n\)の比に内分するといい、点\(P\)を内分点といいます。
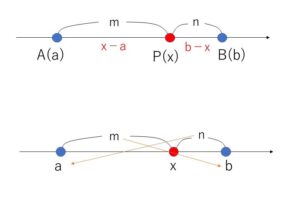
では、数直線上の2点\(A(a)\),\(B(b)\)に対して、線分\(AB\)を\(m:n\)の比に内分する点\(P(x)\)の座標を求めてみると
\(b>a\) のとき
図より
\((x-a):(b-x)=m:n\)
\(n(x-a)=m(b-x)\)
\((m+n)x=na+mb\) だから
\(x=\displaystyle\frac{na+mb}{m+n}\)・・・①
また、\(a>b\)のときも同様にして同じ式が得られます。
特に、\(m=n=1\) のとき点\(P\)は線分\(AB\)の中点となりその座標は
\(x=\displaystyle\frac{a+b}{2}\) です。
\(A(a)\)に対して遠いほうの比\(n\)との積\(na\)と、\(B(b)\)に対して遠いほうの比\(m\)との積\(mb\)を考え、視覚的に覚えるとよいです。
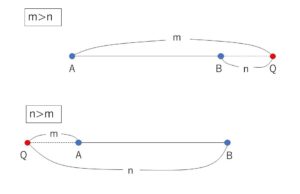
次に外分点について考えていきます。
点\(Q\)が線分\(AB\)の延長線上にあって
\(AQ:QB=m:n\)
が成り立つとき、点\(Q\)は\(AB\)を\(m:n\)の比に外分するといい、点\(Q\)を外分点といいます。
\(m,n\)の大小により\(Q\)の位置が\(A\)側にあるのか\(B\)側にあるのかが変わります。また、\(Q\)は線分\(AB\)の延長線上の点なので、\(m=n\)となることはないため、\(m≠n\) となります。
数直線上での外分点の座標についても求めてみましょう。
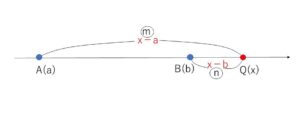
数直線上の2点\(A(a)\),\(B(b)\)に対して、線分\(AB\)を\(m:n\)に外分する点\(Q\)の座標を\(x\)として
(ア)\(b>a\), \(m>n\)のとき
図より
\((x-a):(x-b)=m:n\)
\(m(x-b)=n(x-a)\)
\((m-n)x=-na+mb\) なので
\(x=\displaystyle\frac{-na+mb}{m-n}\)・・・②
他に(イ)\(b>a\),\(m<n\) (ウ)\(a>b\),\(m>n\) (エ)\(a>b\), \(m<n\)
の場合が考えられますが、これらのときも同じ式が得られます。
\(x=\displaystyle\frac{-na+mb}{m-n}\)\(=\displaystyle\frac{(-n)a+mb}{m+(-n)}\)\(=\displaystyle\frac{na+(-m)b}{(-m)+n}\)
となるので、内分点の公式①で \(n→-n\) または \(m→-m\) と置き換えればよいと覚えるといいでしょう。
(例題)
数直線上において、2点\(A(a-1)\),\(B(a+2)\)を結ぶ線分\(AB\)を\(2:1\)の比に内分する点を\(C\)、外分する点を\(D\)とする。
(1)点\(C\)の座標が\(-1\)のときの\(a\)の値を求めよ。
(2)\(a\)が(1)で求めた値のとき、2点\(C,D\)間の距離を求めよ。
(解答)
(1)
\(C\)の座標が\(-1\)なので
\(-1=\displaystyle\frac{1\cdot(a-1)+2\cdot(a+2)}{2+1}\)
\(-3=a-1+2(a+2)\) だから
\(a=-2\)
(2)
\(D\)の座標を外分点の公式より求めて、\(CD\)の距離を出します。
\(A(-3)\),\(B(0)\) なので\(D\)の\(x\)座標は
\(x=\displaystyle\frac{-1\cdot(-3)+2\cdot0}{2-1}\)\(=3\)
よって
\(CD=|3-(-1)|=\)\(4\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→座標平面上の2点の距離と内分・外分