数直線上の2点間の距離、2点の内分点・外分点の知識を利用して、
座標平面上においての2点間の距離、2点の内分点・外分点について考えていきます。
・座標平面上の2点間の距離
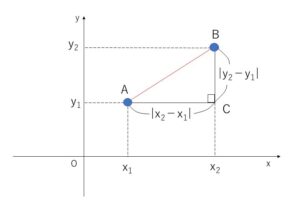
座標平面上の2点\(A(x_1,y_1)\),\(B(x_2,y_2)\)間の距離\(AB\)を考えると
図より
\(AC=|x_2-x_1|\), \(BC=|y_2-y_1|\)
であり、\(△ACB\)は直角三角形なので三平方の定理より
\(AB\)
\(=\sqrt{AC^2+BC^2}\)
\(=\)\(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
となります。
特に原点\(O\)と点\(P(x,y)\)の距離は、\(A(0,0)\),\(B(x,y)\)とすればよいので
\(OP=\sqrt{x^2+y^2}\)
となります。
・座標平面上の2点の内分点・外分点
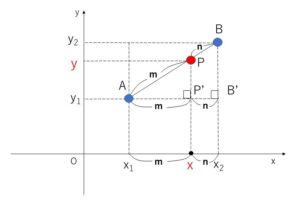
座標平面上の2点\(A(x_1,y_1)\),\(B(x_2,y_2)\)を結ぶ線分\(AB\)を\(m:n\) (\(m,n\)は正の数)の比に内分する点\(P\)の座標\((x,y)\)について考えてみます。
まずは\(P\)の\(x\)座標から考えてみると
図のように、\(P’\),\(B’\)を設定すると
\(AP:PB=AP’:P’B’=m:n\)
よって\(P\)の\(x\)座標は線分\(AB’\)(\(x\)軸に平行)を\(m:n\)に内分する点\(P’\)の\(x\)座標を考えればよいので
\(x=\displaystyle\frac{nx_1+mx_2}{m+n}\)
\(y\)座標についても同様に考えると
\(y=\displaystyle\frac{ny_1+my_2}{m+n}\)
となります。
特に\(m=n=1\) のときは\(P\)は線分\(AB\)の中点となります。
また、線分\(AB\)を\(m:n\)の比に外分する点の座標も内分点と同様に考えると
\(x=\displaystyle\frac{-nx_1+mx_2}{m-n}\)
\(y=\displaystyle\frac{-ny_1+my_2}{m-n}\)
となります。
座標平面上の2点\(A(x_1,y_1)\),\(B(x_2,y_2)\)を結ぶ線分\(AB\)を\(m:n\)の比に内分する点を\(P\)、外分する点を\(Q\)とすると
・\(P\)の座標 \((\displaystyle\frac{nx_1+mx_2}{m+n},\displaystyle\frac{ny_1+my_2}{m+n})\)
・\(Q\)の座標 \((\displaystyle\frac{-nx_1+mx_2}{m-n},\displaystyle\frac{-ny_1+my_2}{m-n})\)
とくに\(AB\)の中点の座標 \((\displaystyle\frac{x_1+x_2}{2},\displaystyle\frac{y_1+y_2}{2})\)
(例題1)
(1)2点\(A(5,4)\),\(B(0,-1)\)について、線分\(AB\)の長さを求めよ。
(2)(1)の2点\(A,B\)について、線分\(AB\)を\(3:2\)の比に内分する点を\(P\),外分する点を\(Q\)とするとき、\(P,Q\)それぞれの座標を求めよ。
(3)直線\(y=3x\)上にあって、2点\(A(1,1)\),\(B(3,0)\)から等距離にある点\(P\)の座標を求めよ。
(解答)
(1)
\(AB=\sqrt{(5-0)^2+(4+1)^2}\)\(=\sqrt{50}\)\(=\)\(5\sqrt{2}\)
(2)
例えば内分点\(Q\)の\(x\)座標は、\(A\)の\(x\)座標\(5\)と\(B\)の\(x\)座標\(0\)について計算します。
内分点Pの座標は
\((\displaystyle\frac{2\cdot5+3\cdot0}{3+2},\displaystyle\frac{2\cdot4+3\cdot(-1)}{3+2})\)\(=\)\((2,1)\)
外分点Qの座標は
\((\displaystyle\frac{-2\cdot5+3\cdot0}{3-2},\displaystyle\frac{-2\cdot4+3\cdot(-1)}{3-2})\)\(=\)\((-10,-11)\)
(3)
\(P\)\((t,3t)\)とおけるので条件より
\(\sqrt{(t-1)^2+(3t-1)^2}\)\(=\sqrt{(t-3)^2+(3t-0)^2}\)
両辺正であり2乗すると
\((t-1)^2+(3t-1)^2=(t-3)^2+(3t)^2\)
これを解くと
\(t=-\displaystyle\frac{7}{2}\)
したがって \(P(-\displaystyle\frac{7}{2},-\displaystyle\frac{21}{2})\)
(例題2)
(1)3点 \(A(3,3)\), \(B(-4,4)\), \(C(-1,5)\)から等距離にある点\(P\)の座標を求めよ。
(2)座標平面上の点\(P(x,y)\)と、 3点 \(A(1,2)\), \(B(5,4)\), \(C(3,6)\) がある。 \(PA^2+PB^2+PC^2\) の最小値およびそのときの点\(P\)の座標を求めよ。
(解答)
(1)
点\(P\)の座標を\(x,y\)とおくと
\(PA^2=PB^2\) より
\((x-3)^2+(y-3)^2=(x+4)^2+(y-4)^2\)
整理すると
\(7x-y=-7\)・・・①
また \(PB^2=PC^2\) より
\((x+4)^2+(y-4)^2=(x+1)^2+(y-5)^2\)
整理すると
\(3x+y=-3\)・・・②
①②より
\(x=-1\),\(y=0\)
したがって \(P(-1,0)\)
(2)
\(P\)\((x,y)\)は座標平面上を自由に動く点で、\(x,y\)はそれぞれバラバラに動きます(\(x,y\)は独立変数)。
\(PA^2+PB^2+PC^2\)
\(=(x-1)^2+(y-2)^2+(x-5)^2+(y-4)^2\)\(+(x-3)^2+(y-6)^2\)
\(=3x^2-18x+3y^2-24y+91\)
\(=3(x-3)^2-27+3(y-4)^2-48+91\)
\(=3(x-3)^2+3(y-4)^2+16\)
よって最小値は\(x=3\),\(y=4\)のとき \(16\) で
このとき \(P(3,4)\)
重心の座標については次回扱います。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→三角形の形状と重心 back→数直線上の2点の距離と内分・外分