座標平面上の3点を結んでできる三角形の形状や重心について見ていきます。
・三角形の重心の座標
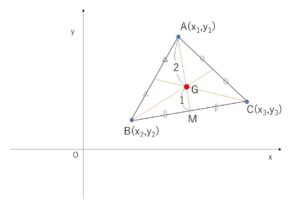
3点\(A(x_1,y_1)\),\(B(x_2,y_2)\),\(C(x_3,y_3)\) を頂点とする\(△ABC\)の重心の座標を求めてみます。
重心\(G\)は\(A\)と\(BC\)の中点\(M\)を結んだ線分\(AM\)を\(2:1\)の比に内分する点です。よってまず中点\(M\)の座標を考えると
\(M(\displaystyle\frac{x_2+x_3}{2},\displaystyle\frac{y_2+y_3}{2})\)
ゆえに、線分\(AM\)を\(2:1\)の比に内分する点\(G\)は
\(G(\displaystyle\frac{1\cdot x_1+2\cdot\displaystyle\frac{x_2+x_3}{2}}{2+1},\)\(\displaystyle\frac{1\cdot y_1+2\cdot\displaystyle\frac{y_2+y_3}{2}}{2+1})\)
となるから、
\(G(\displaystyle\frac{x_1+x_2+x_3}{3},\)\(\displaystyle\frac{y_1+y_2+y_3}{3})\)
(例題1)
2点\(A(1,1)\),\(B(2,5)\)を2つの頂点とし、点\((3,2)\)を重心とする三角形\(ABC\)の頂点\(C\)の座標を求めよ。
(解答)
\(C(x,y)\)とおくと、重心の座標が\(3,2\)なので
\(\displaystyle\frac{1+2+x}{3}=3\), \(\displaystyle\frac{1+5+y}{3}\)\(=2\)
よって \(x=6\),\(y=0\)
答 \(C(6,-0)\)
続いて三角形の形状に関する問題について見ていきます。
(例題2)
(1)3点 \(A(1,-1)\),\(B(4,1)\),\(C(-1,2)\) を頂点とする三角形はどのような三角形であるか調べよ。
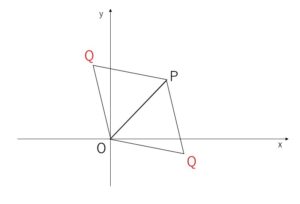
(2)2点 \(O(0,0)\),\(P(2,2)\)に対し、\(△OPQ\)が正三角形となるような点\(Q\)の座標をすべて求めよ。
(解答)
(1)
\(AB^2=(4-1)^2+(1+1)^2=13\)
\(BC^2=(-1-4)^2+(2-1)^2=26\)
\(CA^2=(-1-1)^2+(2+1)^2=13\)
よって\(AB^2+CA^2=BC^2\) より 角\(A\)は\(90°\)
また、\(AB>0,CA>0\) だから
\(AB=CA\)
したがって \(△ABC\)は \(AB=CA\) の直角二等辺三角形
(2)
\(Q(x,y)\)とおくと、\(△OPQ\)が正三角形だから
\(OP^2=OQ^2=PQ^2\)
よって
(ア)\(OP^2=OQ^2\) かつ (イ)\(OP^2=PQ^2\)
(ア)より
\(2^2+2^2=x^2+y^2\)・・・①
(イ)より
\(2^2+2^2=(x-2)^2+(y-2)^2\)・・・②
①-②より
\(0=4x-4+4y-4\)
よって \(y=-x+2\)・・・③
①に代入して
\(8=x^2+(-x+2)^2\)
整理して
\(x^2-2x-2=0\)
ゆえに \(x=1±\sqrt{3}\)
③に代入して
\(y=-(1±\sqrt{3})+2\)\(=1∓\sqrt{3}\)
したがって\(Q\)の座標は
\((1+\sqrt{3},1-\sqrt{3})\),\((1-\sqrt{3},1+\sqrt{3})\)
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→平行四辺形と座標 back→座標平面上の2点の距離と内分・外分