座標を利用した証明について見ていきます。
(例題1)
\(△ABC\)の\(BC\)の中点を\(M\)とするとき
\(AB^2+AC^2=2(AM^2+BM^2)\) (中線定理)
が成り立つことを証明せよ。
できる限り計算が楽な座標をとり方(ただし一般性を失わないとり方)をします。
どんな三角形でも移動させることにより、\(BC\)を\(x\)軸に合わせることができ、さらに\(BC\)の中点を原点\(O\)の位置にもってくることができます。
残りの頂点\(A\)については特に決まった位置にないため\((a,b)\)と設定することになります。
ここで\(A\)を\(y\)軸上に設定すると、\(△ABC\)は二等辺三角形になってしまうので一般性が失われてしまいます。
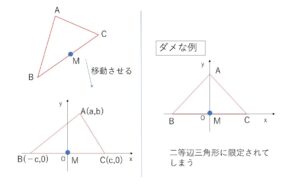
①\(A(a,b)\), \(B(0,0)\),\(C(c,0)\) (1つを原点にもってくる)
②\(A(0,a)\), \(B(b,0)\), \(C(c,0)\) (3つを軸上にもってくる)
などがあります。②は先ほどと違い\(BC\)の中点が原点にあるとは限りません。
(解答)
\(ABC\)を図のように設定する。
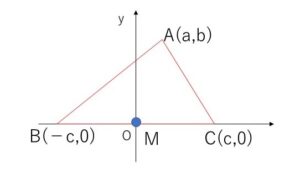
\(A(a,b)\), \(B(-c,0)\), \(C(c,0)\) より
(左辺)
\(=(a+c)^2+b^2+(a-c)^2+b^2\)
\(=2a^2+2b^2+2c^2\)
(右辺)
\(=2(a^2+b^2+c^2)\)
よって(左辺)=(右辺) となり、証明された。
(例題2)
\(△ABC\)と点\(D\)が同一平面上にある。\(DA^2+DB^2+DC^2\)を最小にする点\(D\)は\(△ABC\)の重心であることを示せ。
(解答)
図のように\(ABC\)を設定する。

\(D(x,y)\)とすると
\(DA^2+DB^2+DC^2\)
\(=(x-a)^2+(y-b)^2+(x+c)^2+y^2\)\(+(x-c)^2+y^2\)
\(=3x^2-2ax+3y^2-2by+a^2+b^2+2c^2\)
\(=3(x-\displaystyle\frac{a}{3})^2+3(y-\displaystyle\frac{b}{3})^2\)\(+\displaystyle\frac{2a^2}{3}\)\(+\displaystyle\frac{2b^2}{3}+2c^2\)
よって最小値をとるとき、\(x=\displaystyle\frac{a}{3}\), \(y=\displaystyle\frac{b}{3}\)
\(△ABC\)の重心は \((\displaystyle\frac{a-c+c}{3},\displaystyle\frac{b+0+0}{3})\)\(=(\displaystyle\frac{a}{3},\displaystyle\frac{b}{3})\) であるから
最小値をとる点\(D\)は\(△ABC\)の重心となる。
以上になります。お疲れさまでした。
ここまで見て頂きありがとうございました。
next→直線の方程式 back→平行四辺形と座標